【材料・情報工学向け】ベイズ最適化と機械学習:未踏領域を効率的に探索するAI戦略
📋 目次
- はじめに:材料・情報工学における最適化のフロンティア
- 背景:データ駆動型材料開発と「次元の呪い」
- 機械学習の基礎と最適化の役割
- ベイズ最適化の原理とメカニズム
- 機械学習とベイズ最適化の連携・類似技術との比較
- 応用例:材料工学・情報工学における実践事例
- 将来の展望
- まとめ
- 参考書籍
はじめに:材料・情報工学における最適化のフロンティア
現代の材料開発や情報システム設計において、デジタルトランスフォーメーション(DX)とマテリアルズ・インフォマティクス(MI)は不可欠な概念となっています。AI技術の進化は、材料探索を加速し、新薬開発やロボティクスといった多岐にわたる分野で大きな注目を集めています。
しかし、これらの分野における最適化問題は、多くの場合、目的関数の評価に莫大な時間やコスト、リソースを要します。例えば、新材料の合成実験や複雑なシミュレーションは、1回の試行に多大な労力を伴います。また、多くのパラメータが存在する高次元な探索空間を人間の経験や勘だけで効率的に探索するには限界があります。
このような課題に対し、ベイズ最適化は「少ない試行回数で効率的に最適解に到達する」強力なアプローチとして注目されています。本記事では、材料・情報工学を学ぶ皆様が、このベイズ最適化と機械学習の深い関係性、その基礎から応用、そして将来の展望までを体系的に理解できるよう、詳細に解説していきます。
背景:データ駆動型材料開発と「次元の呪い」
材料開発パラダイムの変革:MIの台頭
20世紀の材料科学は、勘と経験、そして演繹的な手法(結晶構造から物性を計算するなど)が主流でした。しかし、近年ではマテリアルズ・インフォマティクス(MI)と呼ばれるデータ駆動型アプローチが急速に発展しています。MIは、機械学習などの情報科学技術を材料開発に活用し、探索の効率化・高度化を目指すものです。
🔬 MIの具体例
- 無機材料データベース:Materials Projectなどの大規模データベースから物性予測モデルを構築
- 組合せ最適化:合金組成の最適化による高強度材料の開発
- プロセス最適化:製造条件パラメータの調整による品質向上
データ量の課題:「次元の呪い」
MIの成功事例が増える一方で、材料科学分野には特有の課題があります。それは「データ量の少なさ」です。画像認識や言語処理のように大量のデータが利用可能な分野とは異なり、材料開発では実験や計算に高いコストがかかるため、十分なデータを収集することが困難です。
📊 次元の呪いとは
データ数が少ない状況で次元数(データの属性値の数)が増加すると、機械学習モデルの精度が低下する現象。材料の組成、プロセス条件、環境因子など、考慮すべきパラメータが多いほど顕著になります。
この「データ量の少なさ」は、特に次元数(データの属性値の数)が増えると問題が顕著になります。この課題に対処するため、データの少なさを補うための様々な手法が研究されており、その一つがベイズ最適化です。
機械学習の基礎と最適化の役割
機械学習の基本概念
機械学習は「明示的にプログラムしなくても学習する能力を計算機に与える研究分野」と定義されます。その主な目標は、データから学習し、未知の事象に対して判断や予測を行うモデルを構築することです。
重要な概念として、「汎化(Generalization)」と「過学習(Overfitting)」があります。汎化とは、未知のデータに対して正しく予測する能力を指し、機械学習の最終目標は汎化誤差の最小化と言い換えられます。一方、過学習は、学習データに過剰に適合しすぎた結果、未知のデータに対する予測性能が低下する現象です。
ハイパーパラメータと最適化の必要性
機械学習モデルの性能を最大限に引き出すためには、ハイパーパラメータの適切な設定が不可欠です。
| パラメータタイプ | 特徴 | 例 |
|---|---|---|
| 学習パラメータ | モデルの学習過程で自動的に決定 | 線形回帰の係数、ニューラルネットワークの重み |
| ハイパーパラメータ | 事前に人間が設定する必要 | 学習率、層の数、正則化の強さ、決定木の深さ |
このハイパーパラメータの調整は、機械学習における最適化問題の一種です。最適化とは、「特定の集合上で定義された関数について、その値が最小または最大となる状態を選択すること」を指します。
min f(x) subject to x ∈ X
(制約条件Xのもとで関数f(x)を最小化する問題)
特に、目的関数の具体的な形が不明な場合や、勾配情報が利用できない場合、あるいは評価に時間がかかる場合は「ブラックボックス最適化」と呼ばれます。ハイパーパラメータ最適化は、まさにこのブラックボックス最適化の典型的な例です。
ベイズ最適化の原理とメカニズム
ベイズ最適化とは:効率的な探索戦略
🎯 ベイズ最適化(Bayesian Optimization, BO)
評価に高コストがかかるブラックボックス関数の最適解を、できるだけ少ない試行回数で効率的に見つけるための強力な手法。材料探索、プロセス最適化、機械学習のハイパーパラメータ調整など、1回の実験やシミュレーションに多大な時間や費用がかかる分野で威力を発揮。
ベイズ最適化の二つの柱
ベイズ最適化は、主に以下の二つの要素によって駆動されます:
代理モデル(Surrogate Model)
未知の目的関数を確率モデルで近似するものです。多くの場合、ガウス過程回帰が用いられます。ガウス過程は、観測されたデータ点から、未評価の領域における関数の期待値(予測平均)と不確実性(予測分散)の両方を予測します。この不確実性の情報が、ベイズ最適化の最大の強みです。
獲得関数(Acquisition Function)
代理モデルから得られた予測平均と不確実性の情報を用いて、次に評価すべき最適な候補点を決定するための関数です。獲得関数は「探索(Exploration)と活用(Exploitation)のトレードオフ」をバランス良く実現するように設計されます。
| 戦略 | 目的 | 重視する要素 |
|---|---|---|
| 活用(Exploitation) | 既知の最良の結果を迅速に改善 | 予測平均が高い領域 |
| 探索(Exploration) | より優れた解の発見 | 予測分散が大きい未探索領域 |
代表的な獲得関数には、期待改善量(Expected Improvement, EI)や上側信頼限界(Upper Confidence Bound, UCB)などがあります。
ベイズ最適化のサイクル
ベイズ最適化は以下のステップを繰り返すことで機能します:
- 初期データの収集:いくつかの点で目的関数を評価し、初期データを取得
- 代理モデルの構築:取得したデータを用いて、目的関数の代理モデル(通常はガウス過程)を構築
- 獲得関数の最大化:代理モデルから計算される獲得関数を最大化することで、次に試すべき候補点を決定
- 目的関数の評価:決定した候補点で実際に実験やシミュレーションを行い、目的関数の真の値を観測
- モデルの更新:新しい観測データを既存のデータセットに追加し、代理モデルを更新
- 繰り返し:最適解が見つかるか、設定された試行回数に達するまでステップ2〜5を繰り返し
他の最適化手法との対比:グリッドサーチ
ハイパーパラメータ最適化でよく用いられる手法にグリッドサーチがありますが、ベイズ最適化とは大きく異なります:
| 手法 | 探索方法 | 効率性 | 適用場面 |
|---|---|---|---|
| グリッドサーチ | 網羅的に全組み合わせを試行 | 低(試行回数が多い) | 低次元・計算コストが低い場合 |
| ベイズ最適化 | 統計モデルに基づく逐次探索 | 高(試行回数が少ない) | 高次元・計算コストが高い場合 |
このため、ベイズ最適化は試行回数を大幅に削減でき、結果として計算時間が短縮されるという大きなメリットがあります。特に、評価に時間やコストがかかる問題においては、ベイズ最適化の効率性が際立ちます。
機械学習とベイズ最適化の連携・類似技術との比較
ベイズ最適化は、機械学習を「道具」として利用しながら、その機械学習モデル自身の性能を向上させる「メタ学習」のような役割も果たします。
ハイパーパラメータ最適化における中核技術
ベイズ最適化は、機械学習モデルのハイパーパラメータチューニングにおいて、最も代表的かつ効果的な手法の一つです。ディープラーニングのような多数のハイパーパラメータを持つモデルでは、グリッドサーチのような網羅的探索は非現実的であり、ベイズ最適化による効率化が必須となります [Kotthoff et al., 2021]。
能動学習との関連
🎓 能動学習(Active Learning)
教師あり学習において、モデル自身が「次にどの入力データに対する出力ラベルを収集したいか」を能動的に決定する枠組み。ベイズ最適化と同様に、予測の不確実性を情報として活用することで、効率的に学習を進めることが可能。
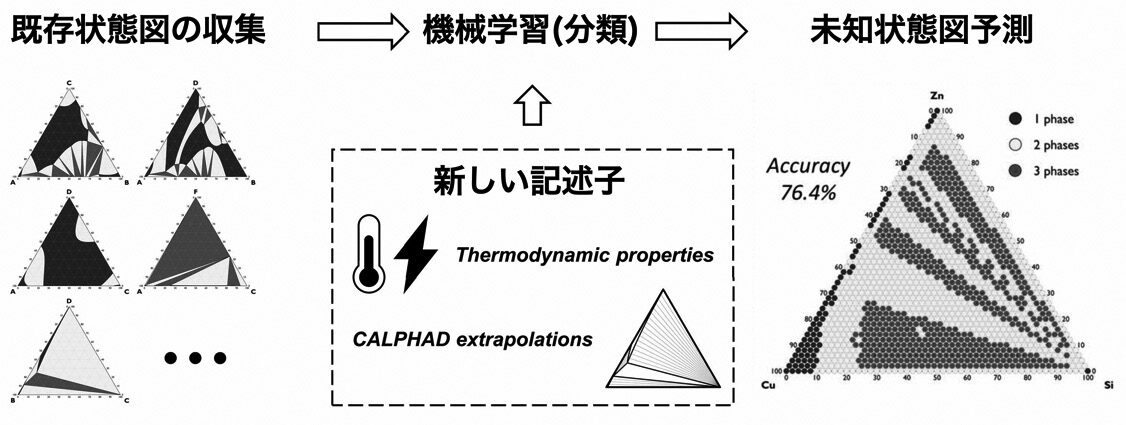
例えば、材料の状態図作成において、不確かな点を機械学習で見つけ出し、次の実験候補として選定する手法が開発されています。
転移学習とマルチタスク最適化
データが少ない問題を補うもう一つのアプローチとして、転移学習(Transfer Learning)があります。これは、過去に集めた類似データを活用して、現在のタスクの学習を効率化する手法です。
🔄 マルチタスクベイズ最適化(MTBO)
複数の最適化問題を並列に解くことを目的とし、ある最適化問題で得られた特徴を他の問題に転移させることで、少ないデータ点で高精度な応答曲面を獲得し、効率的な最適解探索を実現します。計算コストの高い解析モデルの最適化計算において、低コストモデルの学習結果を転移させることで、計算時間を大幅に短縮する事例があります。
その他の類似・関連技術
- 量子アニーリング:組み合わせ最適化処理を高速かつ高精度に実行すると期待されている計算技術で、結晶構造予測に応用する研究も進められています
- 生成AI/LLM:ChatGPTに代表される大規模言語モデル(LLM)は、材料科学分野でも論文や特許からのデータ収集、物性予測モデルの代替、自動・自律型実験システムの構築などに活用されています
応用例:材料工学・情報工学における実践事例
材料開発における応用
🏭 新材料探索とプロセス最適化
ニッケル・コバルト基超合金原料粉末のガスアトマイズ法のプロセス最適化にベイズ最適化が活用され、微細粉末の収率向上を実現し、コスト削減にも成功しています [松井, 2019]。
⚗️ 組成設計
- 高充填率を達成する粒径比率の短時間での探索
- 熱伝導特性に優れた高分子の分子設計
- 低熱ヒステリシス形状記憶合金の探索研究では、未探索領域のデータ点のモデル品質向上寄与を定量化し、効率的な探索を可能にしました
🔬 イオン伝導経路の推定
プロトン伝導体の伝導度推定において、ガウス過程モデルと動的計画法を組み合わせたベイズ最適化により、イオン伝導経路の推定を効率的に行い、計算コストを大幅に削減できることが示されています。
製造業における応用
📈 スケールアップ時の操業条件最適化
化学工学分野では、パイロットスケールからコマーシャルスケールへの製造設備のスケールアップ時に、少ない実験回数で操業条件を最適化するためにベイズ最適化が活用されています。
🔧 製品設計とプロセス調整
プラント配管の延性き裂進展予測モデルのパラメータ調整にマルチタスクベイズ最適化を応用することで、従来の2ヶ月を要した作業をわずか3日に短縮できた事例があります。カーエアコン用送風機の形状最適化においても、全圧効率の最大化と騒音レベルの最小化という多目的最適化にベイズ最適化が用いられ、優れた最適形状を発見し、実測でも改善効果が実証されています [SCSK, 2024]。
情報工学における応用
🤖 機械学習モデルのハイパーパラメータチューニング
ディープニューラルネットワークの隠れ層のニューロン数、活性化関数、学習率、バッチサイズ、Epochsなどのハイパーパラメータを、グリッドサーチよりも短い計算時間で最適化できた事例が報告されています。
⚙️ 制御系設計
PIDゲインの調整など、制御系設計のパラメータチューニングにベイズ最適化を適用することで、業務効率化が期待されています。
将来の展望
ベイズ最適化は、その強力な最適化能力とデータ効率性から、今後も様々な方向で発展が期待されています。
🔮 高次元・大規模問題への対応
現在のベイズ最適化は数次元程度の最適化が限界とされている課題がありますが、バッチ最適化や並列最適化、重要な次元を特定できるスケーラブルなモデルの開発により、より高次元の問題への対応が進むと期待されています。
⚛️ 量子計算との融合
量子機械学習の発展に伴い、ベイズ統計においても推論計算の高速化のための量子アルゴリズムの適用が注目されています。特に、複雑なモデルの推論計算はベイズ統計の大きな障壁であり、将来的に量子コンピュータがその高速化に貢献する可能性があります。
🔬 自動実験システムとの連携
ロボットによる自動実験システムとベイズ最適化を組み合わせることで、人間の介入を最小限に抑えた完全自動化された材料探索システムの実現が期待されています。これにより、24時間稼働での効率的な材料開発が可能になります。
まとめ
ベイズ最適化は、評価コストの高い材料・情報工学の分野において、ガウス過程による不確実性のモデリングと探索と活用のバランスを取る獲得関数を特徴とする、極めて強力なツールです。
機械学習との深い関係において、ベイズ最適化はハイパーパラメータチューニングの中核技術として機能するとともに、能動学習や転移学習といった関連技術との連携により、データが少ない状況での学習効率を大幅に向上させます。
新材料の発見、製造プロセスの最適化、高性能な情報システムの設計など、未踏の領域を効率的に開拓するために、ベイズ最適化は今後ますますその重要性を増していくでしょう。ぜひこの強力なAI戦略を習得し、皆様の研究開発に役立ててください。
参考書籍
以下に、ベイズ最適化と機械学習に関する理解を深めるためのおすすめ書籍を5冊ご紹介します。これらの書籍は、基礎から応用までをカバーしており、オンラインストアで広く購入可能です。


.png)
.png)
v2.png)
.png)
.png)
.png)
.png)
.png)

コメント