はじめに|マテリアルズ・インフォマティクスとは?
MIの定義と歴史
マテリアルズ・インフォマティクス(Materials Informatics、以下MI)は、材料科学と情報技術を融合させた新しい学問分野です。材料科学における実験データやシミュレーションデータを解析し、新材料の発見や既存材料の改良を効率化するための手法です。MIの定義は、膨大な材料データを整理・解析し、機械学習や人工知能(AI)を活用して材料の特性を予測することと言えます。
MIの歴史は2011年、NIST(米国国立標準技術研究所)が司令塔となって始動しました。次いで、ヨーロッパやアジア諸国でも同様のプロジェクトが国の主導で行われました。日本では、2015年にNIMSを拠点として「情報統合型物質・材料開発イニシアティブ」を開始、次いでJSTやNEDOがMI関連プロジェクトを開始しています。
ビッグデータの解析技術や機械学習アルゴリズムの進化により、MIの重要性が急速に高まっています。これにより、従来の材料研究の枠を超えた新しいアプローチが可能となり、材料開発のスピードと効率が劇的に向上していくことが予想されます。
ここで、情報や計算を用いた工学的手法として「シミュレーション」もあります。
いずれも実験回数や試作回数を減らすなどの目的は共通する一方、明確な違いもありますので、しっかりおさえておきましょう。
目標達成の手段
- 材料の性質を司る方程式を解く(シミュレーション・計算科学)
- 材料の性質の「相関関係を表すモデル」を作る(インフォマティクス・情報科学)
MIとシミュレーションのアプローチの違い
- MI:帰納法(既存データから相関関係を見つける)
- シミュレーション:演繹法(原理・法則 → 方程式・近似式)
注意点
機械学習にいおいて、入力→出力の関係(帰納的)から何らかの物理化学的法則(演繹的)な素晴らしいモデルが見つかる可能もある。
but、何の意味もない相関が得られることもあるので注意
例)その地域の納豆の消費量とオリンピックメダリスト輩出者数
MIが解決する問題
MIは、従来の材料開発プロセスにおける以下のような問題の解決が期待されています。
- 膨大なデータの処理
- 新材料の発見
- 材料特性の予測
材料科学においては、多くの実験データやシミュレーションデータが生成されますが、その膨大なデータを効率的に解析するのは困難です。MIは、これらのデータを効果的に整理し、重要なパターンを見つけ出す手助けをします。
新材料の発見には多くの時間とコストがかかりますが、MIを活用することで、データに基づいた予測モデルを構築し、効率的に新材料を発見することが可能になります。
材料の特性を予測することは、材料開発において重要なステップです。MIは、既存のデータを活用して特性予測モデルを構築し、実験回数を減らしながらも高精度な予測を実現します。
MIが材料科学にもたらす効果
MIは、材料科学にもたらす効果として以下の点が挙げられます。
- 開発速度の向上
- コスト削減
- 精度の向上
データ解析と機械学習を駆使することで、新材料の開発サイクルを大幅に短縮します。
無駄な実験を減らし、効率的な研究開発を実現することで、材料開発にかかるコストを削減します。
多くのデータを基にした予測モデルは、高い精度で材料特性を予測できるため、より優れた材料を見つけ出す可能性が高まります。
MIの応用分野
MIの応用分野は非常に広範です。代表的な応用分野として以下が挙げられます。
- エネルギー材料
- 医療材料
- 構造材料
- ナノ・薄膜材料
リチウムイオン電池や燃料電池など、エネルギー変換および保存に関わる材料の研究において、MIは重要な役割を果たしています。特に、エネルギー密度や寿命の向上を目的とした材料開発において、研究が進んでいます。
バイオマテリアルや医療用デバイスに用いられる材料の設計・開発にもMIが活用されています。例えば、体内での分解特性や生体適合性を持つ新しい材料の発見に貢献しています。
高強度・高耐久性を持つ材料の開発においても、MIは重要な手法として利用されています。自動車や航空機などの産業で使用される材料の軽量化と強度向上を目指す研究において、大きな効果を発揮しています。
ナノスケールの材料特性の予測や、薄膜材料の組成制御のツールとしてMIが利用されています。コンビナトリアル実験との併用で、より効率的な物性取得が実現化されています。
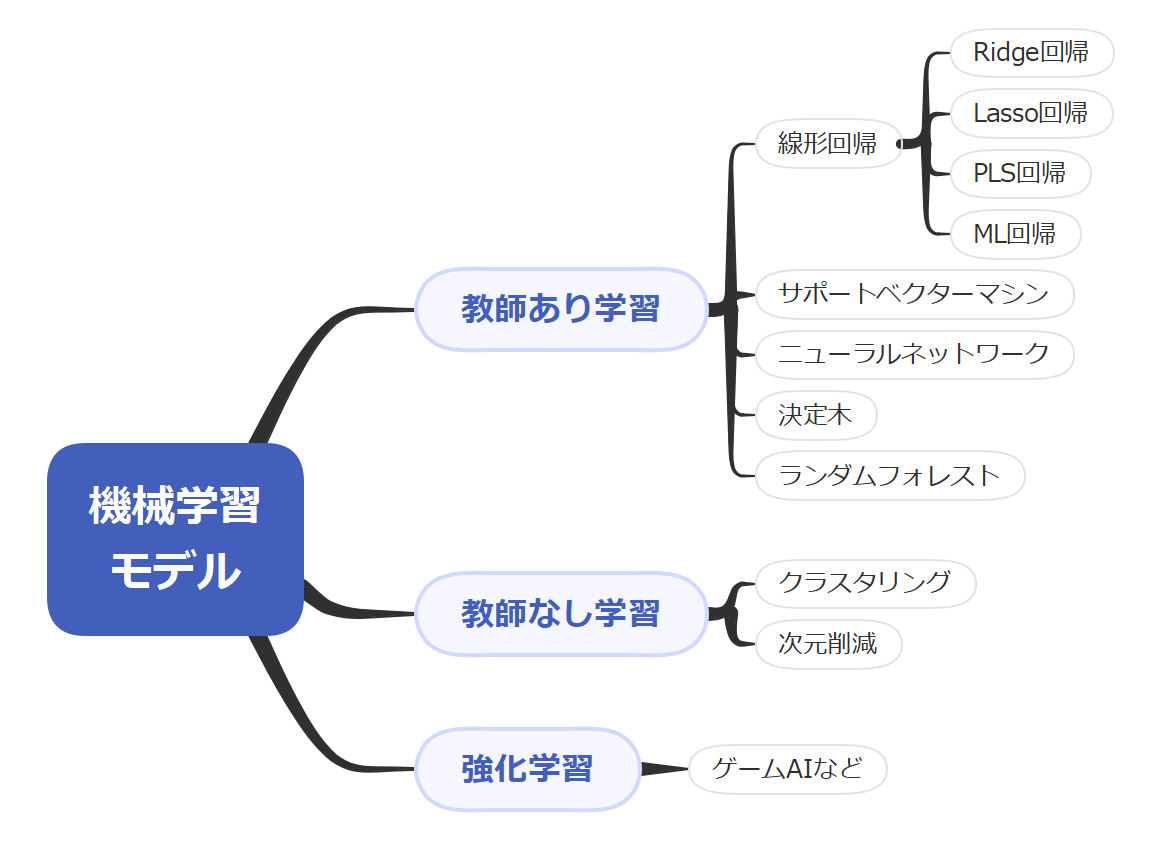
機械学習の種類
そもそも機械学習モデルって何でしょう。
簡単に表現すると…
モデルをfという関数とする
- 様々な材料の特徴量:x
- 実験値yとする
- 未知の材料の実験結果を予測できる
特徴量:\(x_{1}, x_{2}, x_{3}・・・\) → 学習モデルfに代入
※材料の特徴量xを無理やりでも数値化する → yとの相関が取れる
「物質の性質(実験結果)をコンピュータ内で予測すれば望む性質をもつ物質をコンピュータ内で探索できる」
いといったイメージである。
もう少し深く掘り下げましょう。
MIにおいて使用される機械学習には、主に以下の3つの種類があります。
教師あり学習
教師あり学習は、入力データと対応する正解データ(ラベル)を用いてモデルを訓練する方法です。代表的な手法として、線形回帰やサポートベクターマシン(SVM)、ニューラルネットワーク(NN)などがあります。
イメージとしては、
- 入力)(x)と出力(y)をセットで用意
- 相関性を学習させる
→未知の特徴量(x)を入力した際の出力(y)を予測させる
※出力が連続:回帰, 出力が不連続orカテゴリ:分類
※MIで一般的に用いる手法
ex.)スパムメールの識別、犬・猫の写真の識別
となります。
さらに、教師あり学習の代表的モデルを紹介します。
線形回帰
線形回帰は、入力変数と出力変数の間の線形関係をモデル化する手法です。シンプルでありながら、効果的な予測を行うことができます。特に、材料特性の予測においては、その簡便さと解釈性から広く用いられています。
サポートベクターマシン(SVM)
SVMは、データを高次元空間にマッピングし、最適な分離超平面を見つけることで分類や回帰を行います。特に非線形問題に対して強力な手法であり、材料データの分類や回帰において高い性能を発揮します。
ニューラルネットワーク(NN)
ニューラルネットワークは、生物の神経細胞を模したモデルであり、多層パーセプトロンやディープラーニングとして知られています。複雑な非線形関係をモデル化する能力があり、材料特性の予測や新材料の発見において非常に有用です。
教師なし学習
教師なし学習は、ラベルなしのデータを用いてデータの構造やパターンを見つけ出す方法です。
教師なし学習には以下のような特徴があります。
-
- 教師あり学習でいうところの教師(y)がない機械学習
- 入力xをたくさん与えると、xの性質に関し何らかの結果を返す
- データの特徴を学習
- 制御は困難
- 結果の意味の解釈も困難
※MIで最初に取り掛かる手法ではない
※MIにおいては、データがたくさんあるが何をしたらいいかわからない時に使える
以上のように、本記事のメイントピックであるMIには関連が薄いですが、代表的手法をサラっと紹介します。クラスタリングや次元削減手法が一般的です。
クラスタリング
クラスタリングは、データを似た特徴を持つグループに分ける手法です。材料データの中で類似した特性を持つ材料をグルーピングすることで、新たな材料クラスターの発見や分類に役立ちます。
次元削減
次元削減は、多次元のデータを低次元に変換する手法です。主成分分析(PCA)やt-SNEなどが代表的な手法です。次元削減により、データの視覚化や特徴抽出が容易になり、材料データの解析が効率化されます。
強化学習
強化学習は、エージェントが環境との相互作用を通じて報酬を最大化するための行動を学習する方法です。
ゲームAI(将棋、囲碁など)のようなコンピュータ同士の対戦からデータ抽出するなどに応用されています。
エージェントの訓練
エージェントは、試行錯誤を繰り返しながら最適な行動を学習します。材料科学においては、材料合成プロセスの最適化や新材料の発見に向けた実験計画の策定に利用されます。
環境との相互作用
強化学習では、エージェントが環境との相互作用を通じて学習を進めます。材料実験のシミュレーションを通じて、効率的な実験プロトコルの設計や材料特性の最適化を実現します。
MIにおいても強化学習は使える手法ですが、メジャーなのはやはり「教師あり学習」となります。
MIで使われる機械学習モデル
MIでは、様々な機械学習モデルが使用されます。以下に代表的なモデルを紹介します。
いずれものモデルも共通している点は
- データを集める(なるべく多く)
- \(y=f(x)\)となるようなfを作る
材料(説明変数x)と性質(目的変数y)のデータセット
関数fは「説明変数xと目的変数yを関連付ける何らかのモデル」」という広い意味で捉える
となります。
線形回帰
線形回帰は、入力変数と出力変数の間の線形関係をモデル化する手法です。
もう少し詳述すると、
既知のデータセット\((x_{i}, y_{i})\)(i=1,・・・n)に対して、yがxの一次関数で表現できる場合(\(y=a_{x}+b\))で表現できる場合)、「線形関係にある」といいます。
と表せる場合、δiを最小化するような(a,b)を求めれば、未知のxに対するyの値を予測することができます。
- yが1種の説明変数xで表現できる場合:単回帰分析
- yが2種以上の 〃 :重回帰分析
係数(a,b)をどう決めるか?
(xi, yi)における近似直線からの差(残差δi)を最小にしたい
残差の二乗和sが最小値をとるような(a, b)を決定する:最小二乗法
→\(δ_{s}/δ_{a} = 0, δ_{s}/δ_{b} = b_{0}となる(a, b)を探せばよい(下に凸の二次関数の極小値)\)
以上が線形回帰の大枠の指針です。
線形回帰には、細かく分けると以下のような種類があります。
Ridge回帰
Ridge回帰は、制限付き線形回帰の一種で、以下のような特徴があります。
- 回帰係数の二乗の合計をなるべく小さくする(L2正規化と呼ぶ)
- 利点:不自然に大きな係数が出ないため、データに過剰適合するのを防ぐ
- 特に多重共線性が存在する場合に有効
後に詳しい手順は紹介しますが、IDEを利用して機械学習を実行する際のPythonコード例の一部を示します。
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)
predictions = ridge.predict(X_test)Lasso回帰
Losso回帰も、制限付き線形回帰の一種で、以下のような特徴があります。
- 回帰係数の絶対値の合計をなるべく小さくする(L1正規化と呼ぶ)
- 利点:0になる係数が出てくるので、どの説明変数が重要か解釈しやすくなる
Pythonコード例の一部を示します。
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)
predictions = lasso.predict(X_test)PLS回帰
PLS回帰(Partial Least Squares回帰)は、説明変数と目的変数の両方を低次元空間に投影し、その空間での線形回帰を行う手法です。多次元データの解析に適しています。
Pythonコード例の一部を示します。
from sklearn.cross_decomposition import PLSRegression
pls = PLSRegression(n_components=2)
pls.fit(X_train, y_train)
predictions = pls.predict(X_test)MLR
多変量線形回帰(Multiple Linear Regression、MLR)は、複数の説明変数と目的変数の間の関係をモデル化します。シンプルながら効果的な手法で、材料特性の予測に広く使用されています。
Pythonコード例の一部を示します。
from sklearn.linear_model import LinearRegression
mlr = LinearRegression()
mlr.fit(X_train, y_train)
predictions = mlr.predict(X_test)SVM (Support Vector Machine)
サポートベクターマシン(SVM)は、分類および回帰分析に使用されるモデルです。非線形データの処理に優れ、カーネル関数を使用して高次元空間にマッピングすることで、複雑なデータパターンを捉えることができます。
データを非線形写像で変数変換(一言でいえば、「なんとか非線形にしよう」ということ)を行いますが、単純に、非線形性を取り入れようと思ったら、計算量が激増
\(y = px_{a} + qx_{b} + rx_{a}^{2} + sx_{a}^{3} + tx_{b}^{2} + ux_{b}^{3} + vx_{a}x_{b} + wx_{a}^{2}x_{b} + ・・・\)←計算が多くてめんどくさいことになります。
そこで、「カーネルトリック」(数学的手法)を用いることで、変数変換をせずに回帰の結果の係数だけを求めることが可能になります。
代表的カーネル(非線形写像の種類)
- 多項式カーネル
- ガウシアンカーネル
説明変数の特定の次数までの全多項式\((X^{2}, x^{3}, x^{4}, x^{5})\)
(別名:radial basis function(RBF)カーネル) \(exp(-a||x-x’||^{2})\)
※どのカーネルが一番いいかは、誰もわからない
∴あらゆるカーネルを順次試して、最も予測精度の高いもの(評価関数の評価が高い)モデルが最良ということとなる)
Pythonコード例の一部を示します。
from sklearn.svm import SVR
svm = SVR(kernel='rbf', C=1.0, epsilon=0.2)
svm.fit(X_train, y_train)
predictions = svm.predict(X_test)NN (Neural Network)
ニューラルネットワーク(NN)は、生物の神経細胞を模したモデルであり、特にディープラーニングが注目されています。多層のニューラルネットワークを用いることで、複雑な非線形関係を学習し、高精度な予測を行います。
特徴を以下に整理します。
✓非線形写像を多重化
隠れ層を導入し、重み付き和の計算を繰り返し行う
⇒線形回帰を複雑化(関数の中に関数を入れ子にするイメージ)
- 通常の線形回帰:\(y = w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3}\)
- \(Neural Network:y = f(f_{1}(x_{1}, x_{2}, x_{3}), f_{2}(x_{1}, x_{2}, x_{3}), f_{3}(x_{1},x_{2},x{3})\)
\(入力(x_{1}, x_{2}, x_{3}) → 重みづけ(w_{1}, w_{2}, w_{3}) → 出力y\)
\(y = f(x_{1}, x_{2}, x_{3})\)
※重みwは定数
\(入力(x_{1} ,x_{2}, x_{3}) → 隠れ層{(h_{1-1}, h_{1-2}) → (h_{2-1}, h_{2-2}) → (h_{3-1}, h_{3-2})} → 出力y\)
上記のように、「隠れ層」を導入し重み付き和の計算を繰り返し行う
✓出力 = 入力の重み付き和 + 活性化関数
- 活性化関数:tanh, reluなどの非線形関数
- 層が多いほど複雑な学習が可能になる ∴深層学習
ex.) \(h_{1-1} = tanh(w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3})\)
tanh:-1~1までを非線形でとりうる関数、raru:0~入力xの値を非線形でとりうる関数
※いわゆるdeep learningはデータ数が膨大(イメージ、データ数1万じゃ心もとない。1億くらいあればOK)
2~3層程度ならそんなに多くなくてもOK
MIにおいては、そんなにデータが集められないのでDLは不向き
Pythonコード例の一部を示します。
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
model.add(Dense(64, input_dim=X_train.shape[1], activation='relu'))
model.add(Dense(64, activation='relu'))
model.add(Dense(1, activation='linear'))
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(X_train, y_train, epochs=50, batch_size=10, verbose=1)
predictions = model.predict(X_test)決定木(けっていぎ)
決定木は、データを特徴に基づいて分類・回帰するシンプルで解釈しやすいモデルです。ツリー構造を用いてデータを分割し、予測を行います。
以下のような特徴があります。
- Yes/ Noでこたえられる分岐で構成された階層的な木構造を構築
- 分岐の数と閾値をさまざまに変えて入力データに最適化
- 分類木(分類に使う場合)、回帰木(回帰に使う場合)に呼び分ける場合もある
- 過学習に注意
Pythonコード例の一部を示します。
from sklearn.tree import DecisionTreeRegressor
tree = DecisionTreeRegressor()
tree.fit(X_train, y_train)
predictions = tree.predict(X_test)RF (Random Forest)
ランダムフォレスト(RF)は、複数の決定木を用いたアンサンブル学習の一種です。バギングを用いて複数の決定木を訓練し、その予測結果を平均化することで、過学習を防ぎつつ高精度な予測を実現します。
以下のような特徴があります。
- 決定木の過学習を改良した版
- 複数の機械学習を組み合わせ、より強力なモデルを構築する(アンサンブル法)
- N個の決定木の多数決(分類の場合)、または平均値(回帰の場合)を予測結果に用いる
- 1つの決定木が過学習によって妥当性を欠いていても、たくさん決定木を作るので最終的に良好なモデルができる
- 結構うまくいくことが多く、初心者も手を付けやすいのが特徴
※欠点として、「外挿」が不得意
Pythonコード例の一部を示します。
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=100)
forest.fit(X_train, y_train)
predictions = forest.predict(X_test)これまで示した機械学習モデルを含め様々なモデルが存在しますが、それらの特徴は一長一短。どれが一番優れているというモノではありません。
そのことを、分かりやすくまとめると、「予測性能」と「モデル解釈性」の二軸でとらえてマトリックスにすることができます。
下に、各学習モデルの位置づけを示します。
材料開発において、真のモデルに近い機械学習モデルが欲しい場合と、とにかく予測性能の高いモデルが欲しい場合があります。
人間が中身を解釈し現象を解析するためには、「モデルの解釈性」も求められるますし、理屈は抜きでいいからとにかく精度よく予測したいときは「予測性能」を重視します。
内挿と外挿
- 内挿
- 外挿
ある既知の数値データを基にして、そのデータ列の各区間の範囲内を埋める数値を求めること
ある既知の数値データを基にして、そのデータの範囲の外側で予想される数値を求めること
※外挿の精度を上げたい場合、極力「モデルを単純化」することが大事
∴線形回帰のような単純なモデルを構築する発想が重要
MIの開発環境
MIの開発には、ノーコードツールやコーディングが必要なツールが存在します。それぞれの環境について説明します。
ノーコードでの開発環境
ノーコード開発環境は、プログラミングの知識がなくても機械学習モデルを構築できるツールです。
※ノーコード:プログラミング言語を用いずGUI(Graphical User Interface)を用いたプログラミング手法
以下に代表的なソフトを紹介します。
- NNC
- Matrix Flow
- Azure Machine Learning Studio (classic)
NNC(Neural Network Console)は、ソニーが提供するノーコードツールで、ドラッグアンドドロップでニューラルネットワークを設計できます。直感的なインターフェースを持ち、初心者でも簡単に使用できます。

Matri Flowは、データフロー型のノーコードプラットフォームで、データの前処理から機械学習モデルの構築までを一貫して行えます。ビジュアルプログラミングにより、複雑なデータ処理を簡単に実装できます。

Azure Machine Learning Studioは、Microsoftが提供するクラウドベースのノーコードプラットフォームです。データセットのインポートからモデルの訓練、評価までを一貫して行え、ビジネスユーザーやデータサイエンティストにとって使いやすい環境です。
コーディングが必要な開発環境(本記事で詳しく解説する方法)
本記事では、詳しく解説する(というか、オススメする)方法は、コーディングが必要な方法です。
もちろん万人にススメするわけではありませんが、5-1)で紹介したようなノーコードでGUIを用いた環境にはない、以下のような希望がある方ならおススメします。
- クラウドで動かしたい(PCに色々ソフトを入れたくない、マシンスペックに依存したくない)
- とにかく無料で使いたい
- コーディング(文字を打ち込んでプログラムを組む)してみたい
コーディングが必要な開発環境は、柔軟なカスタマイズが可能で、複雑なモデルや高度な解析を行う際に適しています。
必要な環境| たったこれだけ!
結論、皆さんに整えていただきたい環境はこの2つだけ。
- Excel:データを集める
- Google Colaboratory(or Anaconda)
→Pythonを動かす環境 + 機械学習ライブラリ
無料とは言いましたが、Microdsoft Excel(有料)は恐らく皆さんのPCに既にインストール済みかと思いますのでご愛嬌を。
Google Colaboraoryは、便利な機能と豊富なリソースを兼ね備えた機械学習の学習に最適なプラットフォームです。 ブラウザ上でPythonコードの実行環境を提供し、ユーザーは自身のマシンに何もインストールすることなく機械学習のコーディングを行うことができる便利で手軽なツールです。
上記で(Anaconda)と書きましたが、聞いたことがない方は気にしなくてOKです。
ただ、もしプログラミング経験者で既にAnacondaがPCにインストール済みなどの方は、こちらをGoogle Colaboratoryの代わりに使用してもいいかもしれません。
プログラミングを始める前に
本記事はプログラミングの解説メインではありませんが、プログラミング初心者の方でも気軽にMIを始めてほしく、でも最低限押さえておきたい超基本事項だけ示しておきます。
- プログラミングとは
- 基本操作
- その他もろもろ必要な操作
手順の明文化
操作を適切な順番で行うよう命令する(=プログラムを書く)
①四則演算(+/-/×/÷)
②変数への代入
③条件分岐
④繰り返し
⑤関数(def)の定義 (⑤’データ設計図(クラス))
⑥ライブラリ(関連する機能(関数・クラス)をまとめたもの)
⑦データの塊の操作(配列・リスト・タプル etc.)
⑧ファイルの読み込み・書き出し
結局プログラミングの要素は上記で書いたことの組み合わせです。難しく考えず、気負わずやってみましょう。
機械学習のプログラミングを上達させるコツは、上から順にマスターしていくのではなく、機械学習で使うライブラリをいきなり使ってみるところから入った方が上達早いです。
既存のプログラムの真似をしてみるところから入ることが定石です!
プログラミング言語
プログラミングも様々ありますが、MIでよく使われる2つを紹介します。
- Python
- R
Pythonは、機械学習およびデータ解析に広く使用されるプログラミング言語です。豊富なライブラリ(scikit-learn、TensorFlow、PyTorchなど)があり、初心者から専門家まで幅広く利用されています。
Rは、統計解析に特化したプログラミング言語です。統計モデルの構築やデータ可視化に優れ、多くのパッケージが提供されています。特に、生物学や医学分野で広く利用されています。
本記事ではPythonを用いて解説します。
エディター(IDE)
プログラムの実行環境として様々なIDE(Integrate Developmet Environment)やエディターと呼ばれるものがあります。
クラウド(インターネットの仮想サーバー上で動かすもの)とローカル(自身のPCにインストールして動かすもの)に大別できます。各々代表的なものを紹介します。
- Google Colaboratory(クラウド)
- Visual Studio Code(ローカル)
Google Colaboratory(Colab)は、Googleが提供するクラウドベースのIDEで、ブラウザ上でPythonコードを実行できます。無料でGPUを利用できるため、計算リソースが必要な機械学習プロジェクトに適しています。
Visual Studio Code(VS Code)は、Microsoftが提供する軽量で強力なコードエディタです。多数の拡張機能があり、PythonやRの開発環境としても優れています。ローカル環境での開発をサポートし、柔軟なカスタマイズが可能です。
本記事ではGoogle Colaboratory(Colab)上での実行例を後ほど解説します。
PythonプログラミングでのMIの実践
Pythonを用いてMIを実践する前にGoogle Colabの使い方を紹介します。
Google Colabの始め方
- Googleアカウントでサインイン
- Google Colabにアクセス
- 新しいノートブックを作成
Google Colabを利用するにはGoogleアカウントが必要です。まだアカウントを持っていない場合は、Googleアカウントを作成してください。
ウェブブラウザで Google Colab にアクセスします。

画面右下の「新しいノートブック」ボタンをクリックします。
基本的な操作
セルの追加と実行
ノートブックはセルと呼ばれるブロックに分かれています。セルにはコードセルとテキストセルがあります。
コードセルにPythonコードを入力して、Ctrl + Enterキーを押すとそのコードが実行されます。
テキストセルはMarkdown形式で記述できます。セルのタイプはツールバーから変更できます。
※Markdown形式とは:
テキストを構造的に記述する「マークアップ言語」の一つです。特定の記号を使って、段落や見出し、装飾などを自動的に表示できます。内容と構造を分けて扱えばいいので、見出しや本文、箇条書きといったレイアウトを気にせず、素早く文章を入力していくことができます。
ライブラリのインストール
必要なライブラリがまだインストールされていない場合、
import ライブラリ名でインストールすることができます。
例えば、pandas(データ解析を容易にする機能を提供するPythonのデータ解析ライブラリ)をインストールする場合、
import pandas as pdでpandasがインストールできます。
ちなみに、後半の「as pd」は「pdとして = 以後、pandasをpdと呼ぶ」といった意味になります。
長ったらしいライブラリ名は冒頭でこのように略称で定義すると後々のコーディングが楽になります。
Googleドライブのマウント
自分のGoogleドライブをColabにマウントすることで、ドライブ内のファイルにアクセスすることができます。
ファイルのアップロード
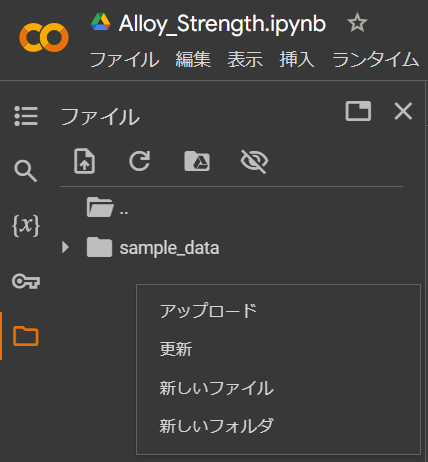
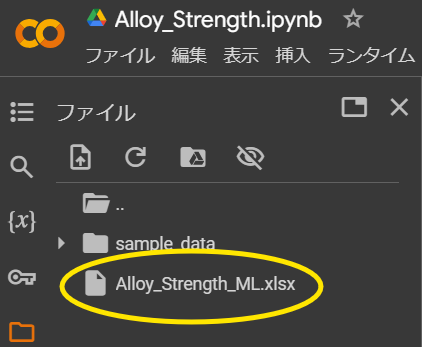
自分のローカルファイルをアップロードすることもできます。下の画像のマウスカーソル位置で右クリックか、ファイルを直接ドラッグしてアップロード可能です。
※アップロードはcsvやxlsxデータから情報を読み取る際に必要です
便利な機能
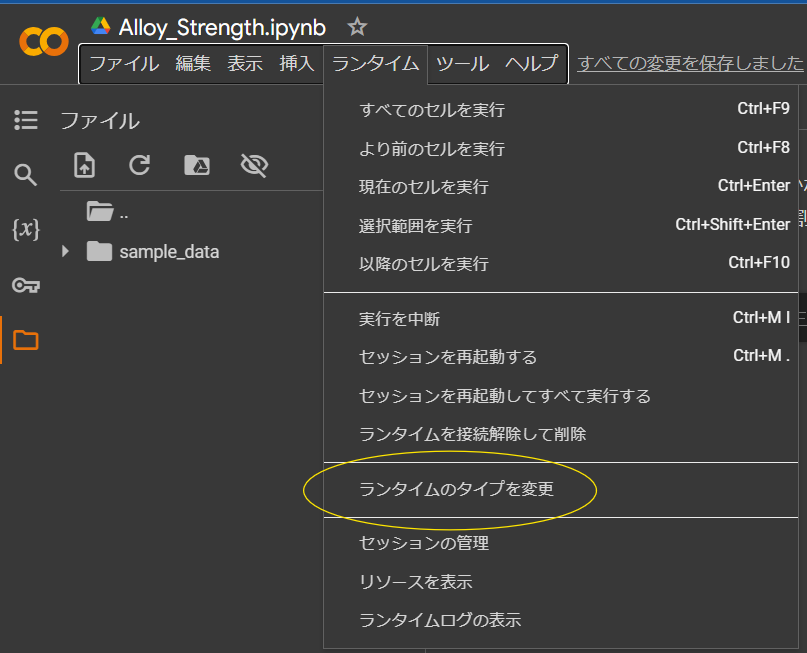
GPU/TPUの利用
高速な計算が必要な場合、ノートブックの環境設定からGPUやTPUを有効にすることができます。「ランタイム」→「ランタイムのタイプを変更」→「ハードウェア アクセラレータ」を「GPU」または「TPU」に設定します。
ノートブックの共有
Google Colabノートブックは簡単に共有できます。右上の「共有」ボタンをクリックしてリンクを生成し、他のユーザーと共有できます。また、他のユーザーがあなたのノートブックにアクセスして一緒に作業することもできます。
サンプルコード|まずは簡単なプログラムを走らせてみよう
以下は簡単なサンプルコードです。NumPyライブラリを使って配列を作成し、Matplotlibライブラリを使ってプロットを表示します。
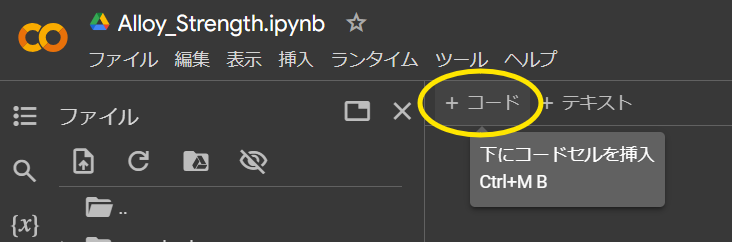
①[+コード]をクリックしてセルを表示させる
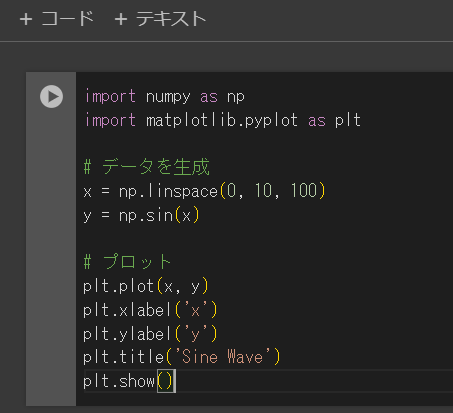
②下記のコードを丸ごとセル上にコピー&ペーストする(細かいことは気にしない)
#ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
# データを生成
x = np.linspace(0, 10, 100)
y = np.sin(x)
# プロット
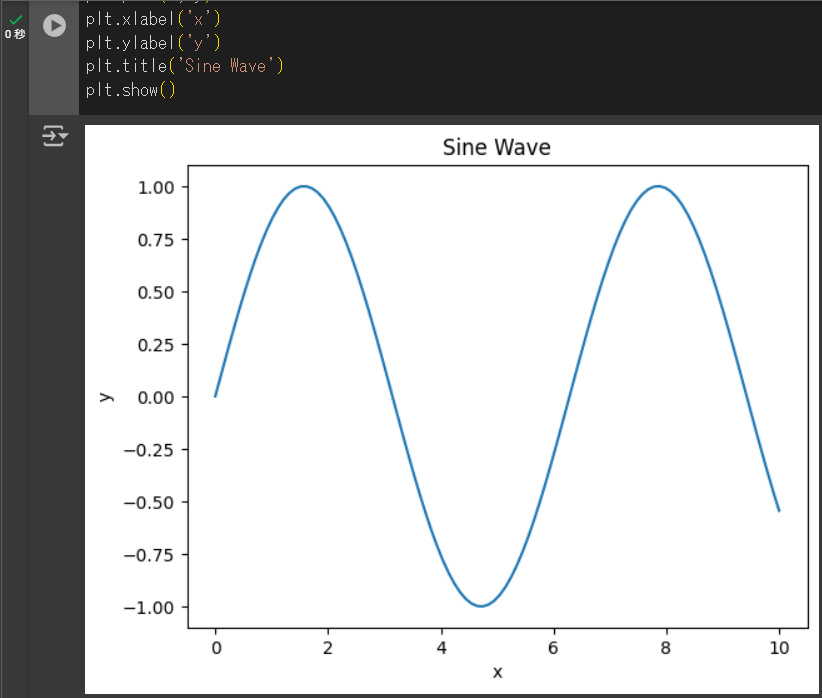
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Sine Wave')
plt.show()↓こんな感じの画面になります
③[セルの実行]をクリック or [Ctrl + Enter]を押す
↓こんなかんじの出力結果になります。
サイン波のグラフを出力するプログラムがこんなに一瞬でできてしまいます。
Pythonのライブラリの威力を感じたのではないでしょうか。
細かい文法や所作については、この記事ではあえて解説を控えます。
優良なコンテンツは他のサイトに多くありますので、ぜひぜひいろいろ調べてみてください。
「習うより慣れろ!!」
プログラミングはこれに尽きます。
これでGoogle Colabの基本的な使い方について説明しました。これを参考にして、MIにおける機械学習のプロジェクトに取り組んでみてください。
PythonプログラミングでのMIの実践|一連のコーディング例
実際のコーディング例を以下に示します。
あくまでデモ的にではありますが、
- 合金元素A, B, Cの%(Element_A, B, C)
- 結晶粒径(Grain_Size)
- 硬さ(Hardness)
- 引張強さ(Tnesile_Strength)
という5つの説明変数から
を予測すること目的としたMIを実行します。
念のため断りとして、今回用いるデータは実際の実験値などは関係ないデタラメなものです。
また、今回は30サンプル分のデータしか用意しませんでしたが、実際はより多くの膨大なデータが必要な場合もあります。
あくまで、流れを理解するためのデモだとご理解ください。
では、let’s try!
step0:ライブラリのインポート
step0ということで、まずは環境の準備としてライブラリの読み込みです。
ライブラリとはその名の通り図書館のように、必要な関数やメソッドをパッケージでまとめたものです。
これらをインポートしておくことで、後々のコーディングがとても楽になります。
まずは何も考えずに、以下の手順を行ってください。
- 下記のコードをコピーする
- Colab上で[+コード]をクリック
- セルに貼り付ける
- 実行する(Ctrl + Enter)
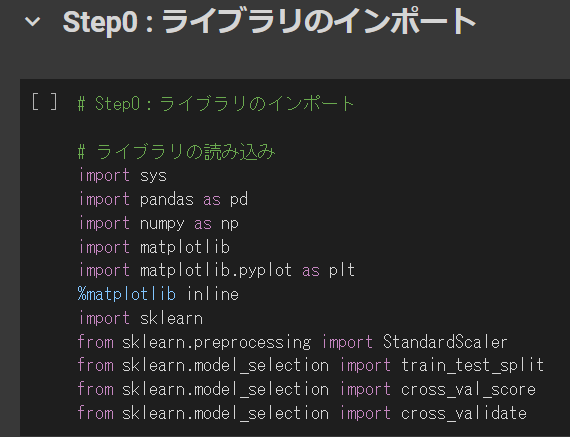
# Step0:ライブラリのインポート
# ライブラリの読み込み
import sys
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import cross_validateこのような画面になればOKです。(特別出力結果が表示されるわけではありません)
1つ補足すると「#」以後の文字列はメモ用(コメント)です。
つまり、「#」をコードのセル中に入力することで、#より右側の文字列は命令には影響しないコメント扱いとなります。
もう一つ補足すると8行目に「import sklearn」というコードがあります。「sklearn(エスケーラーン)というライブラリをインポートせよ」という意味です。
この「sklearn」がPythonを使った機械学習の肝で、これまで紹介してきたような様々な機械学習モデルのアルゴリズムがたくさん収録されています。
どの機械学習モデルを適用するせよとりあえずインポートするライブラリとして是非押さえておきましょう。
step1:データ読み込み
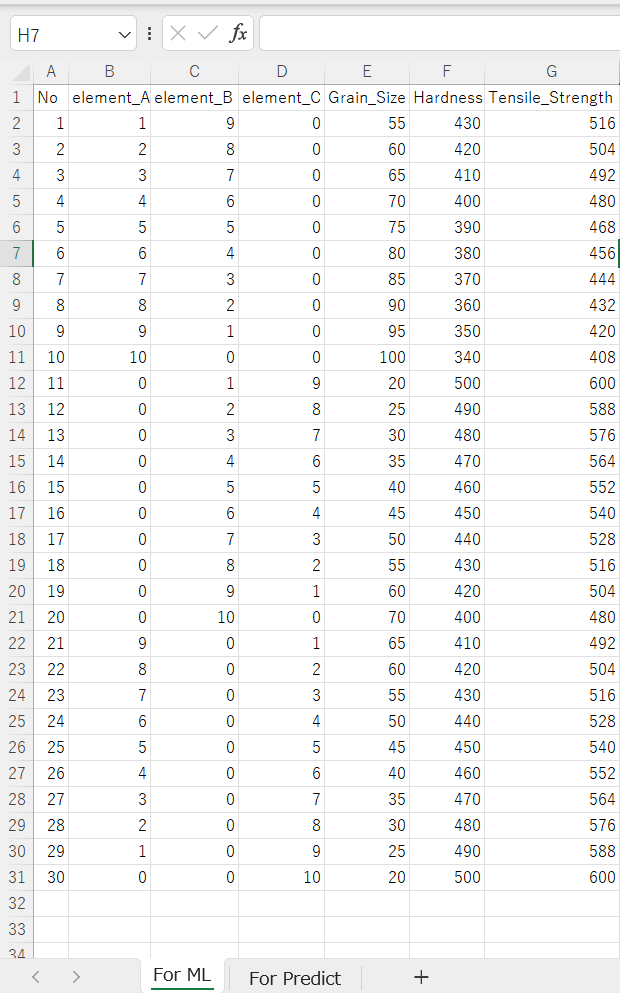
まず、読み込むcsv or xlsxデータを準備します
サンプルデータ(Alloy_Strength_ML.xlsx)の中身はこんな感じです。
非常に重要な点が、シート名を「For ML」としているところです。
後のプログラムに影響しますので、文字列を間違わず、シート名をつけましょう。
自身でデータを入れ込むのが面倒な方は、以下のマークダウン形式の文字列をコピペして、エクセルで開いてください。
| No | element_A | element_B | element_C | Grain_Size | Hardness | Tensile_Strength |
|—-|———–|———–|———–|————|———-|——————|
| 1 | 1 | 9 | 0 | 55 | 430 | 516 |
| 2 | 2 | 8 | 0 | 60 | 420 | 504 |
| 3 | 3 | 7 | 0 | 65 | 410 | 492 |
| 4 | 4 | 6 | 0 | 70 | 400 | 480 |
| 5 | 5 | 5 | 0 | 75 | 390 | 468 |
| 6 | 6 | 4 | 0 | 80 | 380 | 456 |
| 7 | 7 | 3 | 0 | 85 | 370 | 444 |
| 8 | 8 | 2 | 0 | 90 | 360 | 432 |
| 9 | 9 | 1 | 0 | 95 | 350 | 420 |
| 10 | 10 | 0 | 0 | 100 | 340 | 408 |
| 11 | 0 | 10 | 0 | 25 | 490 | 576 |
| 12 | 0 | 9 | 1 | 30 | 480 | 564 |
| 13 | 0 | 8 | 2 | 35 | 470 | 552 |
| 14 | 0 | 7 | 3 | 40 | 460 | 540 |
| 15 | 0 | 5 | 5 | 40 | 460 | 552 |
| 16 | 0 | 6 | 4 | 45 | 450 | 540 |
| 17 | 0 | 7 | 3 | 50 | 440 | 528 |
| 18 | 0 | 8 | 2 | 55 | 430 | 516 |
| 19 | 0 | 9 | 1 | 60 | 420 | 504 |
| 20 | 0 | 10 | 0 | 70 | 400 | 480 |
| 21 | 0 | 10 | 0 | 70 | 400 | 480 |
| 22 | 9 | 0 | 1 | 65 | 420 | 504 |
| 23 | 8 | 0 | 2 | 55 | 430 | 516 |
| 24 | 7 | 0 | 3 | 50 | 440 | 528 |
| 25 | 6 | 0 | 4 | 45 | 450 | 540 |
| 26 | 5 | 0 | 5 | 40 | 460 | 552 |
| 27 | 4 | 0 | 6 | 35 | 470 | 564 |
| 28 | 3 | 0 | 7 | 30 | 480 | 576 |
| 29 | 1 | 0 | 9 | 25 | 490 | 588 |
| 30 | 0 | 0 | 10 | 20 | 500 | 600 |
下の画像のようにアップロードしましょう。
以下の状態になればOK。
また、新たなコードセルを立ち上げて、下記をコピペします。
# Step1:データの読み込み
# 左側メニューの「ファイル」をクリックし、アップロードしたいデータ(csv or xlsxファイル)をドラッグする
# Excelファイルの「For ML」Sheetからデータを読み込んで、dl_MLに代入
# dfは"data frame"の略。
# pythonでは、data frameとarrayの2種類をよく使うので、どちらか混乱しないようにdata frameにはdfと名前を付ける癖をつけるべし
df_ML = pd.read_excel("Alloy_Strength.xlsx", sheet_name='For ML')上記のコードを実行したら、下記をコピペ&実行します。(読み込んだだけですので何も出力されないはずです。)
以下のような画面になればOKです。
続けて、下にセルを追加して以下のコードをコピペ&実行します。
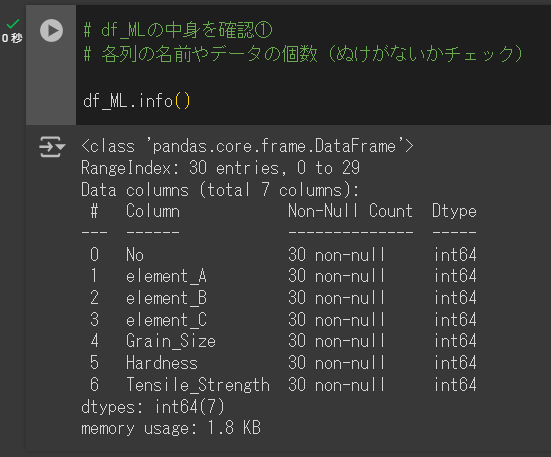
# df_MLの中身を確認①
# 各列の名前やデータの個数(ぬけがないかチェック)
df_ML.info()下記のような画面になればOKです。
ちなみに、中身の確認は特に実行結果に影響はないので飛ばしてもOKですが、念のためアップロードしたファイルが正く読み込まれているかの確認に使うコマンドです。
同じ目的で以下のコードも「セルの追加 → コードのコピペ → 実行」を繰り返して、様々な角度からデータファイルの中身が確認できます。
from google.colab import drive
drive.mount('/content/drive')上記はGoogle Driveをマウント(Colabとファイル共有)するためのコマンドです。
後々便利なので実行しておきましょう。下記のような画面になればOKです。
# df_MLの中身を確認②
# データを上から3行だけ見る head(#)の#の数で行数を指定
df_ML.head(3)下記のような画面になればOK。
# df_MLの中身を確認③
# 念のた全データ(行)確認したい場合は以下のコードを実行する
pd.set_option('display.max_rows', None) #pandasの設定変(行を最大まで表示)
pd.set_option('display.max_columns', None) #pandasの設定変(行を最大まで表示)
print(df_ML) #df_MLの中身を全て表示ここまでやらなくてもOKですが、一応こんなコマンドを使うと全データの確認もできます。
下記のような画面になればOK。
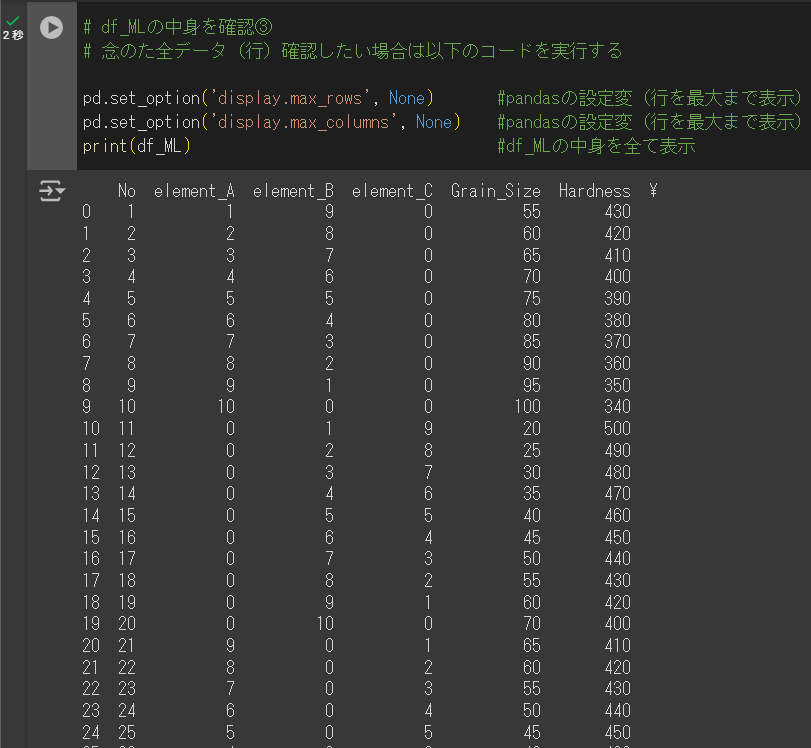
上記の画面は切れて見えますが、一応、No.30まで問題なく表示されているはずです。
step2:データの切り分け
MIで主に用いられる教師あり学習は、データのすべてを学習用に用いるというよりは、訓練用とテスト用に分けて、訓練用で構築した学習モデルをテスト用に適用してみて、その精度を検証します。これお「ホールドアウト検証」と呼びます。
そのため、手持ちのデータを便宜上、訓練用とがテスト用に切り分けする必要がありますが、それを自動で行うプログラムを実行します。
下にセルを追加して以下のコードをコピペ&実行します。
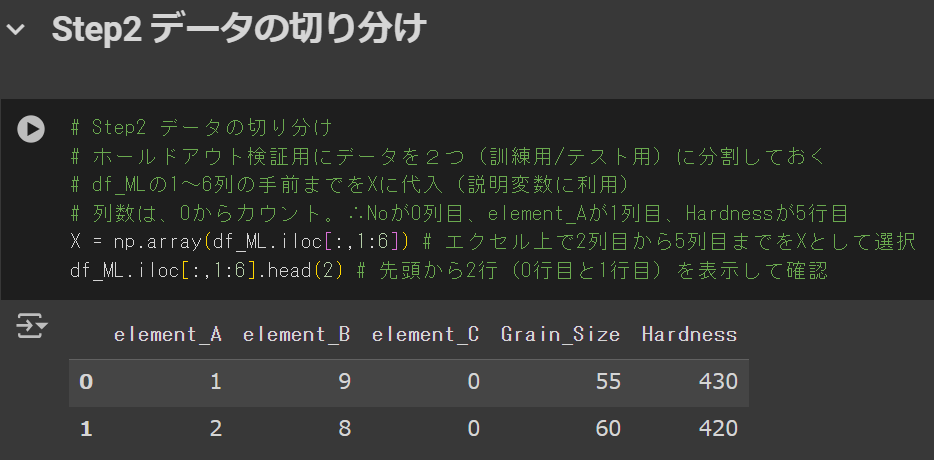
# Step2 データの切り分け
# ホールドアウト検証用にデータを2つ(訓練用/テスト用)に分割しておく
# df_MLの1~6列の手前までをXに代入(説明変数に利用)
# 列数は、0からカウント。∴Noが0列目、element_Aが1列目、Hardnessが5列目
X = np.array(df_ML.iloc[:,1:6]) # エクセル上で2列目から5列目までをXとして選択
df_ML.iloc[:,1:6].head(2) # 先頭から2行(0行目と1行目)を表示して確認下の画像のようになればOKです。
補足すると、
- X(説明変数)として1~5列目を代入
- 先頭の2行を表示して確認
という作業を実行しています。
ちなみに、Pythonは「0スタート」です。上記のコード上で0の数字はエクセル上で1を指しますのでご注意ください。
ここのところ、ちょっとややこしいのでもう少し捕捉します。
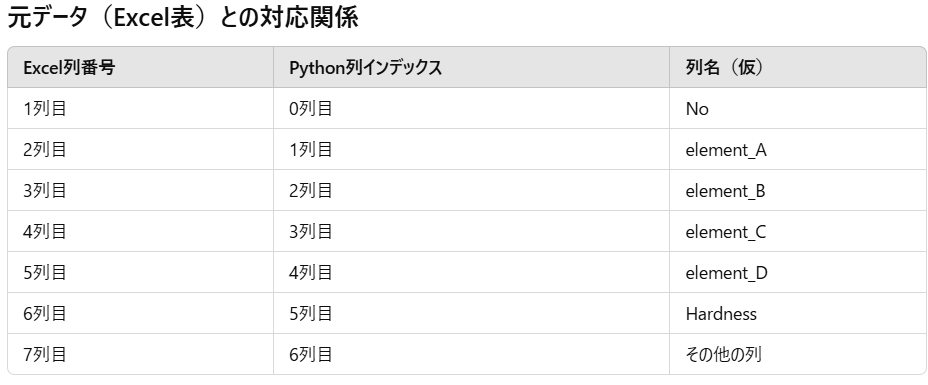
元データ(Excel表)との対応関係を下表にまとめます。
上記のように、元データ(Excel表)状の列数とPython上の列インデックスは、Pythonが0スタートのため1列ズレます。
この「Python = Excel+1」という関係は何列までいっても変わりません。
ではなぜ、iloc[:,1:6]はExcel上で「2列から7列まで」ではなく、「2列から6列まで」指定することになるのか。
この答えは、「iloc のスライスは start:end の end を含まない」ということになります。
つまり、
- Excelでいう「2列目から6列目」
- 7列目(Pythonの6列目)は含まれない(iloc のスライスは start:end の end を含まない)
ということになりますので、ややこしいですが注意しましょう。
続いて、Y(目的変数)の定義とデータの確認のため、下記のコードをコピペ&実行します。
# Tensile_Strengthとラベル付けされた列をYに代入(目的変数に利用)
Y = np.array(df_ML["Tensile_Strength"]) # エクセル上でTensile_Strengthの列をYとして選択
df_ML["Tensile_Strength"].head(2) # Tensile_Strengthの列を2行だけ表示下のような画面になればOKです。
次に、読み込んだX(説明変数)データの標準化を行うため、以下のコードをコピペ&実行する
# 説明変数を標準化(平均を0、分散を1)する ※正規化は最小を0、最大を1にスケーリングする点で異なるので注意
# 標準化は線形回帰の基本。必ずやると思ってよし!
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)上のコードを実行しても特に何かが出力されるわけではありません。
続いて、ホールドアウト検証用にデータを訓練用、テスト用に分けるプログラムを実行します。
下記のコードをコピペ&実行します。
# ホールドアウト検証用にデータを「訓練データ(train)」と「検証用データ(test)」に分ける
# 分け方はランダム(今回は、train : test = 70% : 30% に分ける)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, Y, test_size=0.3)こちらも、何か出力されるわけではありません。
step3:ハイパーパラメータを決定(訓練データを用いてK分割交差検証)
ハイパーパラメータとは、機械学習だけでは決めきれない(人間が決めるしかない)パラメータです。
慣れていないうちは、適当な数字を決定してもいいですが、慣れてきたら妥当な数値を設定できるようにすることを頭の片隅に置きましょう。
では、どのように妥当な値を決定するか。
指針:TrainのデータをさらにK分割交差検証にかける → スコアの平均値が最良となるハイパーパラメータを採用する
まずは、ランダムフォレストのモデルを使用する前提で、下記のコードをコピペ&実行してください。
# Step3 ハイパーパラメータを決定する(訓練データを用いてK分割交差検証)
from sklearn.ensemble import RandomForestRegressor
# RandomForest用にハイパーパラメータを決める
# 訓練用データ(train)を用いて5-fold CV
for ne in range(10,130,20):
for nd in range(2,20,2):
model = RandomForestRegressor(n_estimators=ne, max_depth=nd,random_state=123)
#print("n_estim=", ne, "depth=", nd,"-----------------")
#print(cross_val_score(model, X_train, y_train, cv=5))
print("n_est=", ne, "depth=", nd, "score=", cross_val_score(model, X_train, y_train, cv=5).mean()) # scoreとはR^2値(決定係数)のこと下の画面のようになればOKです。(画像は下が切れていますが、もう少し出力結果が続きます)
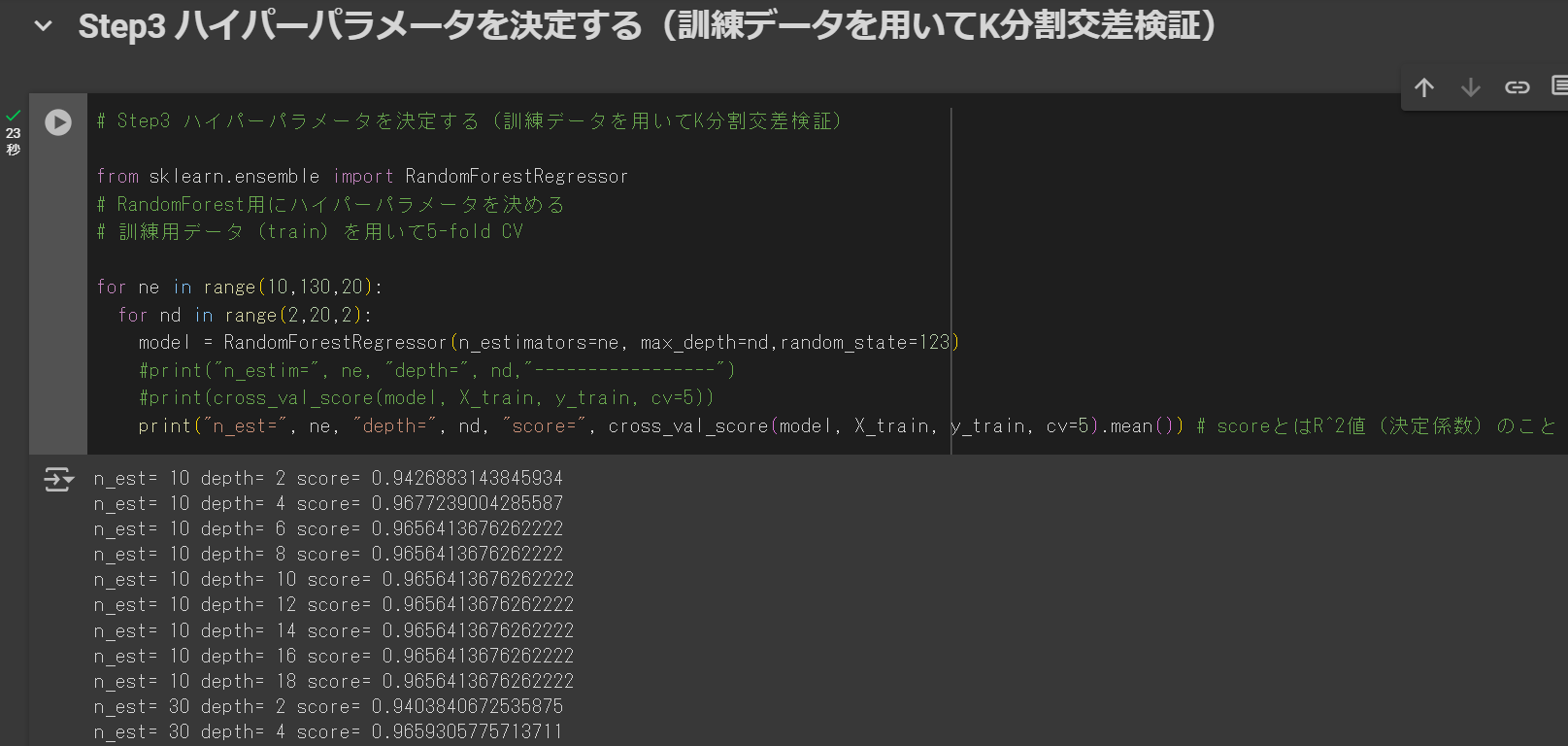
step4:機械学習実行(例.ランダムフォレスト)
いよいよ肝心な機械学習の実行プログラムを走らせます。
といっても、プログラムなんと3行だけ!
以下のコードをコピペ&実行しましょう。
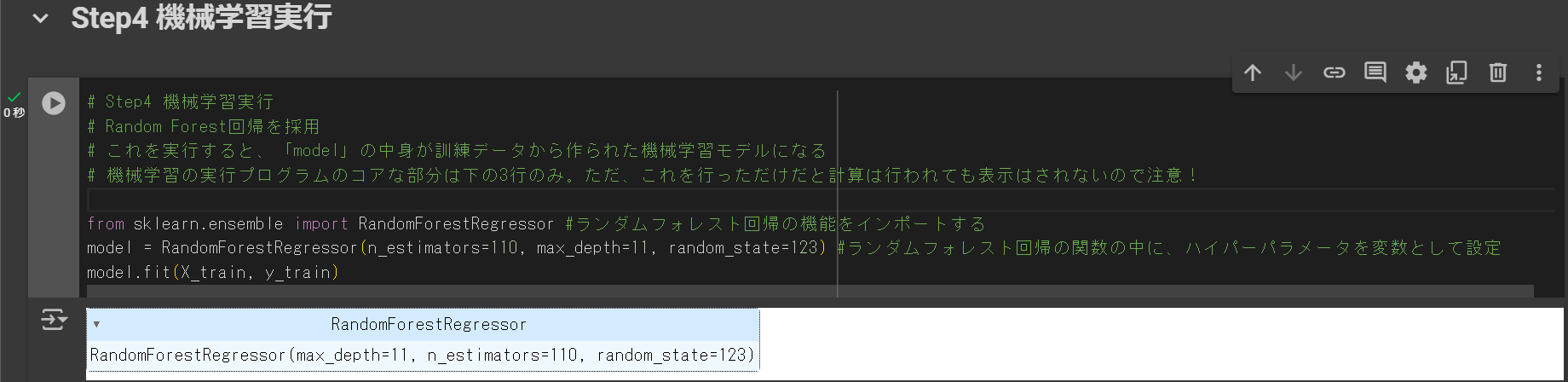
# Step4 機械学習実行
# Random Forest回帰を採用
# これを実行すると、「model」の中身が訓練データから作られた機械学習モデルになる
# 機械学習の実行プログラムのコアな部分は下の3行のみ。ただ、これを行っただけだと計算は行われても表示はされないので注意!
from sklearn.ensemble import RandomForestRegressor #ランダムフォレスト回帰の機能をインポートする
model = RandomForestRegressor(n_estimators=110, max_depth=11, random_state=123) #ランダムフォレスト回帰の関数の中に、ハイパーパラメータを変数として設定
model.fit(X_train, y_train)上記のプログラムを実行し、下のような画面になればOKです。
これだけではよく分かりませんね。
では次に、モデルの妥当性を検証します。
以下のコードをコピペ&実行しましょう。
# 機械学習モデルの妥当性を検証
# 訓練データとテストデータのスコアを見る(スコアが1に近いほど良いモデル)
# ここでのscoreとはR^2値(決定係数)を意味する
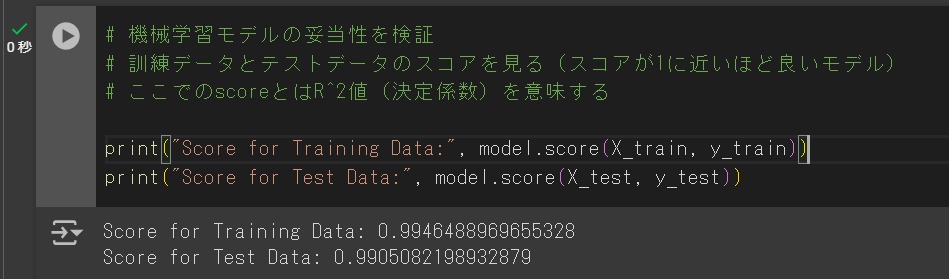
print("Score for Training Data:", model.score(X_train, y_train))
print("Score for Test Data:", model.score(X_test, y_test))下のような画面になればOKです。
出力結果に、
- トレーニング(訓練用)データのスコアが約0.99
- テスト(検証用)データのスコアが約0.99
と表示されています。
スコアとは、決定係数(R^2)のことで、1に近いほどPredict(機械学習モデルから予測される目的変数Y)とTrue(実際の測定値Y)の相関が強いことを表します。
つまり、今回の機械学習モデルは訓練用データも検証用データもスコアが1に非常に近いため、大変良い機械学習モデルであると言えます。
一方、こんな結果が出た場合は以下のように解釈します。
Training Score(訓練用) > Test Score(検証用):オーバーフィッティング(過学習)
→訓練用のデータに学習モデルを合わせ込みすぎている = 汎用性が低い
オーバーフィッティングの要因として以下のようなものが挙げられます。
- データ:データの件数に対し、説明変数(項目、特徴量)が多い
- 学習方法:(疑似的な)未知データの不使用
- 不必要な長時間の学習の実施
- モデル:データに対し、モデルが複雑すぎる
もし、オーバーフィッティングが生じたらハイパーパラメータや学習モデルを調整して何度もトライしましょう。
次に、各説明変数が目的変数に及ぼす寄与度をみるためのプログラムを実行します。
下記のコードをコピペ&実行しましょう。
# Random Forest回帰モデルに対する、各説明変数の重要度を算出
df = pd.DataFrame(model.feature_importances_, index = df_ML.iloc[:, 1:6].columns) # model.feature_imortances_は重要度(各説明変数の寄与度(1以下))を呼び出す関数
print(df)下のような画面になればOK。
上記の結果を見るとGrain_sizeとHardnessの重要度(importance)が他の要因より高めの数字となっている。
また、Element_Cも他のElementより比較的大きい数字のためTensile_Strengthに及ぼす影響は大きいと判断できる。
機械学習の妥当性は、スコアのような数字で判断することも大切ですが、グラフのような視覚的(直感的)に判断することも大切です。
そこで、訓練用データと検証用データ、それぞれの予測値と実測値の相関性を視覚的に見てみましょう。
下記のコードをコピペ&実行してください。
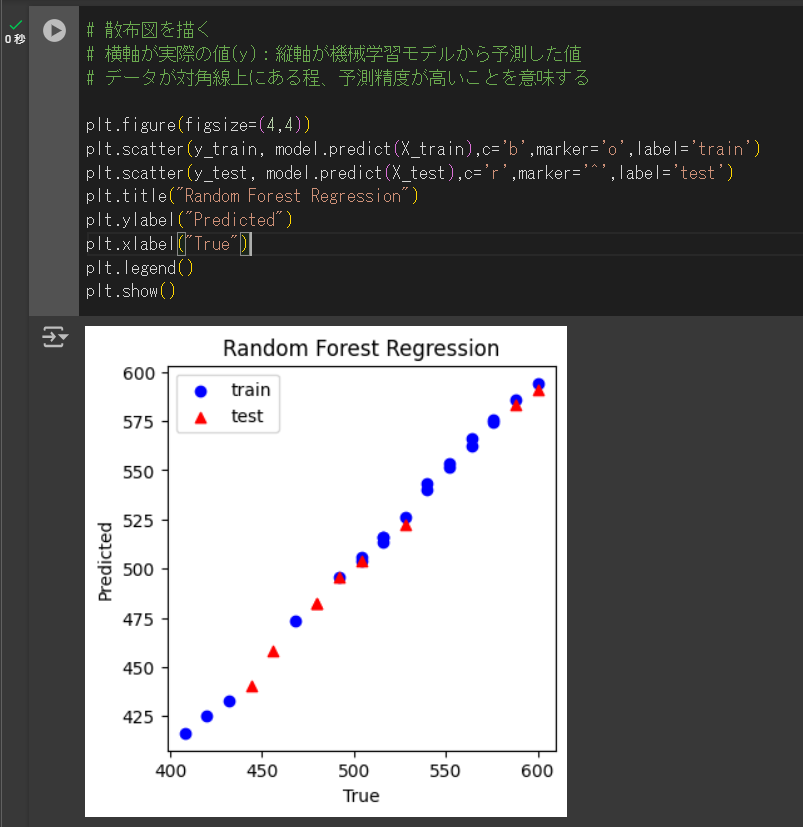
# 散布図を描く
# 横軸が実際の値(y):縦軸が機械学習モデルから予測した値
# データが対角線上にある程、予測精度が高いことを意味する
plt.figure(figsize=(4,4))
plt.scatter(y_train, model.predict(X_train),c='b',marker='o',label='train')
plt.scatter(y_test, model.predict(X_test),c='r',marker='^',label='test')
plt.title("Random Forest Regression")
plt.ylabel("Predicted")
plt.xlabel("True")
plt.legend()
plt.show()以下のような画面になればOKです。
訓練用、検証用、各々線形性が強く良好な学習モデルとなっていると見て取れます。
ここまでが、手元にあるX,Yそれぞれ既知のデータを使った機械学習モデルの構築と精度の検証でした。
いよいよ、目的変数(Y)が未知のデータを使った予測のstepに入ります。
step5:目的変数が未知のデータに対する予測
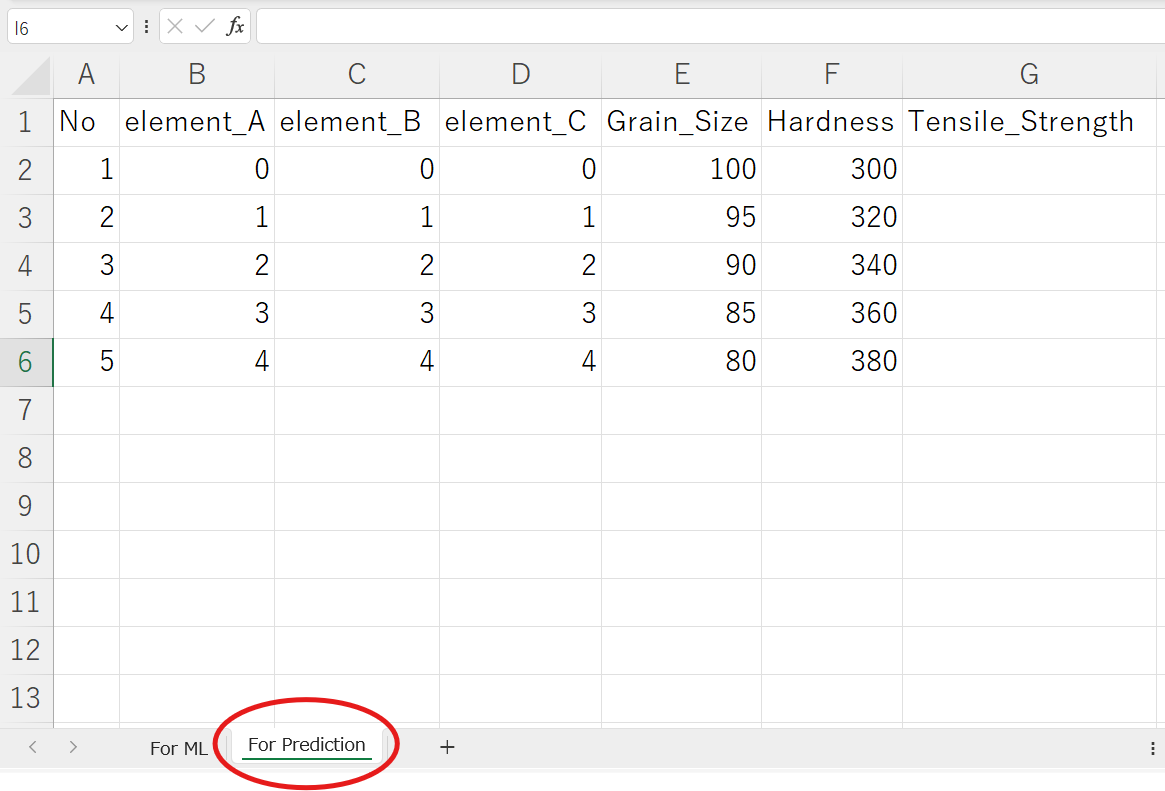
まずは、Excelデータに「For Prediction」タブを追加して説明変数X(Element_A,B,C、Grain_Size, Hardness)を入れます。
今回は、目的変数(Y:Tensile Strength)未知のデータを5つ入れることにします(下図参照)。
For Predictionタブに説明変数を入力したxlsxデータを準備したら、改めてcolb上にそのファイルをアップロードしましょう。
アップロードが終わったら、下記のコードをコピペ&実行します。
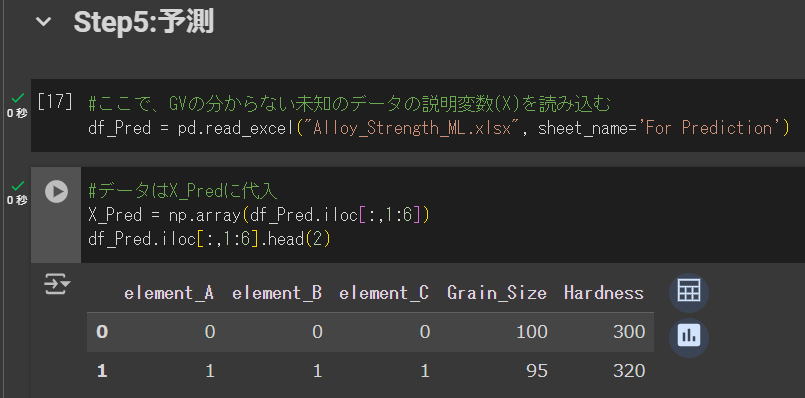
#ここで、GVの分からない未知のデータの説明変数(X)を読み込む
df_Pred = pd.read_excel("Alloy_Strength_ML.xlsx", sheet_name='For Prediction')実行が終わってもデータの読み込みだけなので何か出力されるわけではありません。
次に、念のためデータが正しく読み込まれているか確認するため、以下のコードを実行して先頭の2行のデータを確認します。
#データはX_Predに代入
X_Pred = np.array(df_Pred.iloc[:,1:6])
df_Pred.iloc[:,1:6].head(2)下のような画面になればOKです。
次に、読み込んだ説明変数の数値を正規化するため、下記のコードを実行します。
#説明変数を正規化する
#機械学習モデルを作った時に定義したscalerをそのまま適用
X_Pred_scaled = scaler.transform(X_Pred)上記を実行しても特に出力結果は出ません。
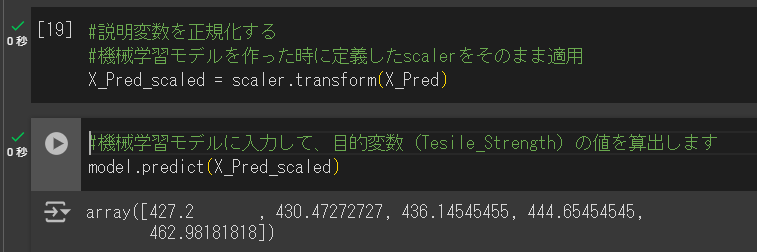
次に、下記のコードを実行して、予測値を出力します。
#機械学習モデルに入力して、目的変数(Tesile_Strength)の値を算出します
model.predict(X_Pred_scaled)下記のような画面になればOKです。
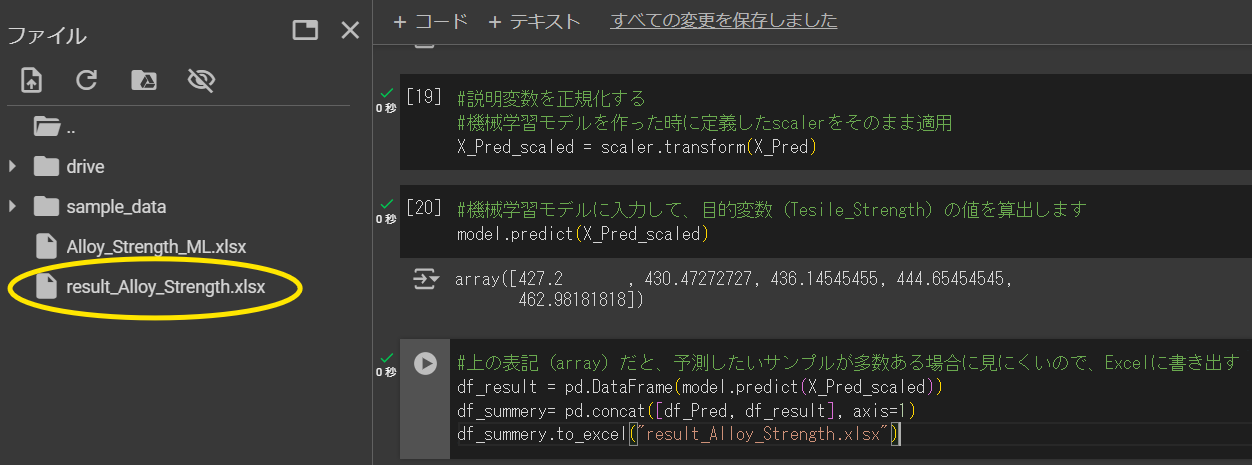
出力結果を参照して終了でもいいのですが、以下のコードを実行するとアップロードしたxlsxファイル(result_Alloy_Strength.xlsx)に結果が出力されます。
#上の表記(array)だと、予測したいサンプルが多数ある場合に見にくいので、Excelに書き出す
df_result = pd.DataFrame(model.predict(X_Pred_scaled))
df_summery= pd.concat([df_Pred, df_result], axis=1)
df_summery.to_excel("result_Alloy_Strength.xlsx")上記を実行すると、clob上のフォルダに指定したファイル名のxlsxデータがアップロードされます。
手動でダウンロードしてもいいですが、下記のコードを実行するとローカルのdownloadフォルダに格納されます。
from google.colab import files
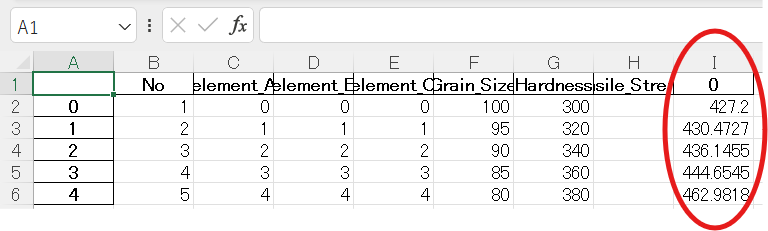
downloaded = files.download("result_Alloy_Strength.xlsx")データの中身はこんな感じ。
以上で「step5 予測」は終了です。
step6:他の学習モデルも試してみよう|Lasso回帰
このステップはおまけですので飛ばして構いません。
学習モデルのブラッシュアップのため、既に試したモデルのハイパーパラメータを調整するなども大切ですが、学習モデル根本から見直すことも大切です。
他の学習モデルとして「Lasso回帰」を例に実行して、ランダムフォレストの結果と見比べてみましょう。
それでは、新たなセルを追加して以下のコードを実行しましょう。
# 機械学習の方法を選択
# 今回はLASSO回帰(解釈性を重視する物性物理の人たちが気に入っている模様)
from sklearn.linear_model import Lasso
model = Lasso(alpha=1.0, max_iter=100000)
# 機械学習実行:ここから後ろは、RandomForestの時と変更なし
model.fit(X_train, y_train)
# 検証
print("Score for Training Data:", model.score(X_train, y_train))
print("Score for Test Data:", model.score(X_test, y_test))
# 散布図描画
plt.figure(figsize=(5,5))
plt.scatter(y_train, model.predict(X_train),c='b',marker='o',label='train')
plt.scatter(y_test, model.predict(X_test),c='r',marker='^',label='test')
plt.title("LASSO Regression")
plt.ylabel("Predicted")
plt.xlabel("True")
plt.legend()
plt.show()
# 回帰係数(5個の条件に対する係数)を表示
print('coeff :', model.coef_)下のような画面になればOKです。
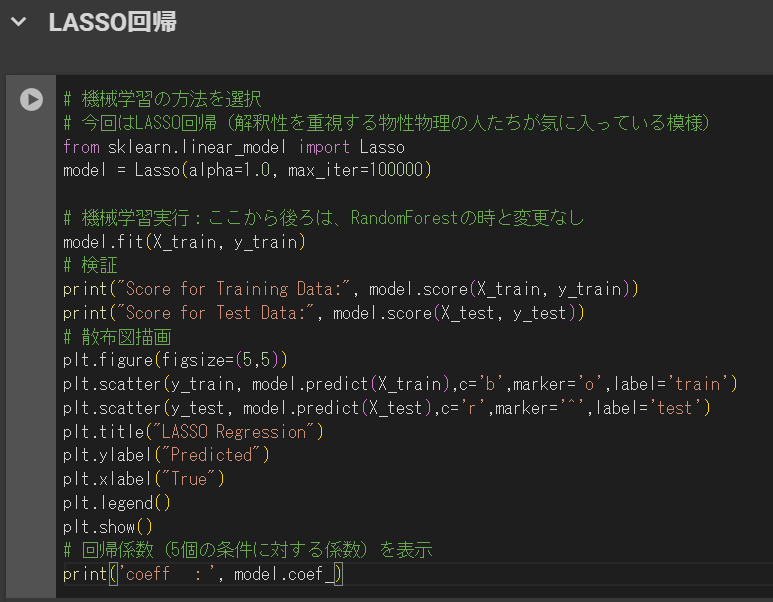
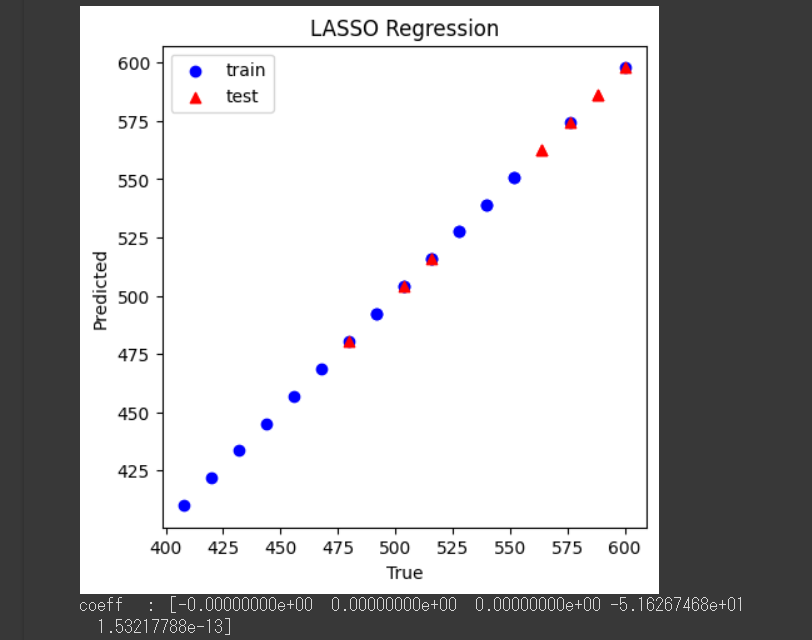
上記のプログラムではスコア、グラフ、係数をセットで出力させています。
スコアは、ランダムフォレストの時と同様、決定係数(R^2)を示します。
グラフを見ると、ランダムフォレストより線形性が強まっていますね。
係数(coeff)は各説明変数の寄与度と考えてください。
係数に着目すると、Element_A, B, Cはほぼゼロで、目的変数(Tensile_Strength)への影響は小さく、Grain_Sizeはマイナスに、Hardnessはプラスに寄与していることが分かります。
このように、LASSO回帰はモデルの解釈性に優れているのが特徴です。
Pythonの「sklearn」というライブラリでは、他にも様々な機械学習モデルをサポートしていますのでいろいろと試してみてください。
まとめ
マテリアルズ・インフォマティクスは、材料科学と情報技術を融合させた新しい分野であり、膨大なデータを活用して新材料の発見や既存材料の改良を効率化する手法です。機械学習の様々な手法を用いることで、材料特性の予測や分類を高精度に行うことができます。Pythonを用いた具体的な実践方法を通じて、MIの基本的な概念と技術を理解することができますのでぜひチャレンジしてみましょう!
書籍紹介
「マテリアルズインフォマティクス|材料開発のための機械学習超入門」著者:岩崎悠真 氏、出版社:日刊工業新聞社
「実践 マテリアルズインフォマティクス」著者:船津公人氏、柴山翔二郎氏、出版社:近代科学社
以上の書籍は、MIの基礎から実践までを学ぶための優れたリソースです。興味を持った方は、ぜひ手に取ってみてください。












コメント