はじめに|言語データの構造的に整理することの威力
QC7つ道具については、「聞いたことくらいはある」という人は多いのではないでしょうか。
でも、「新QC7つ道具」についてはいかがでしょうか。
QC検定(品質管理検定)受験経験者などは勉強したことがあるでしょう。
「”新”てつくから何か新しいの?」
という印象がありますが、そういう意味ではありません。
QC7つ道具は主に数値データを扱うものが多かったのですが、新QC7つ道具は主に言語データを扱います。
新QC7つ道具は以下の7つになります。
- 親和図法
- 連関図法
- 系統図法
- PDPC法
- アローダイアグラム
- マトリックス図法
- マトリックスデータ解析法
自身の頭の中身を整理するときはもちろん、グループディスカッションなどで出た意見をまとめたりする際にも超有効ですので是非覚えてください。
私は材料系技術者ということもあり、主に金属材料の製造・開発・評価などの場面を想定した例を示しながら解説します。
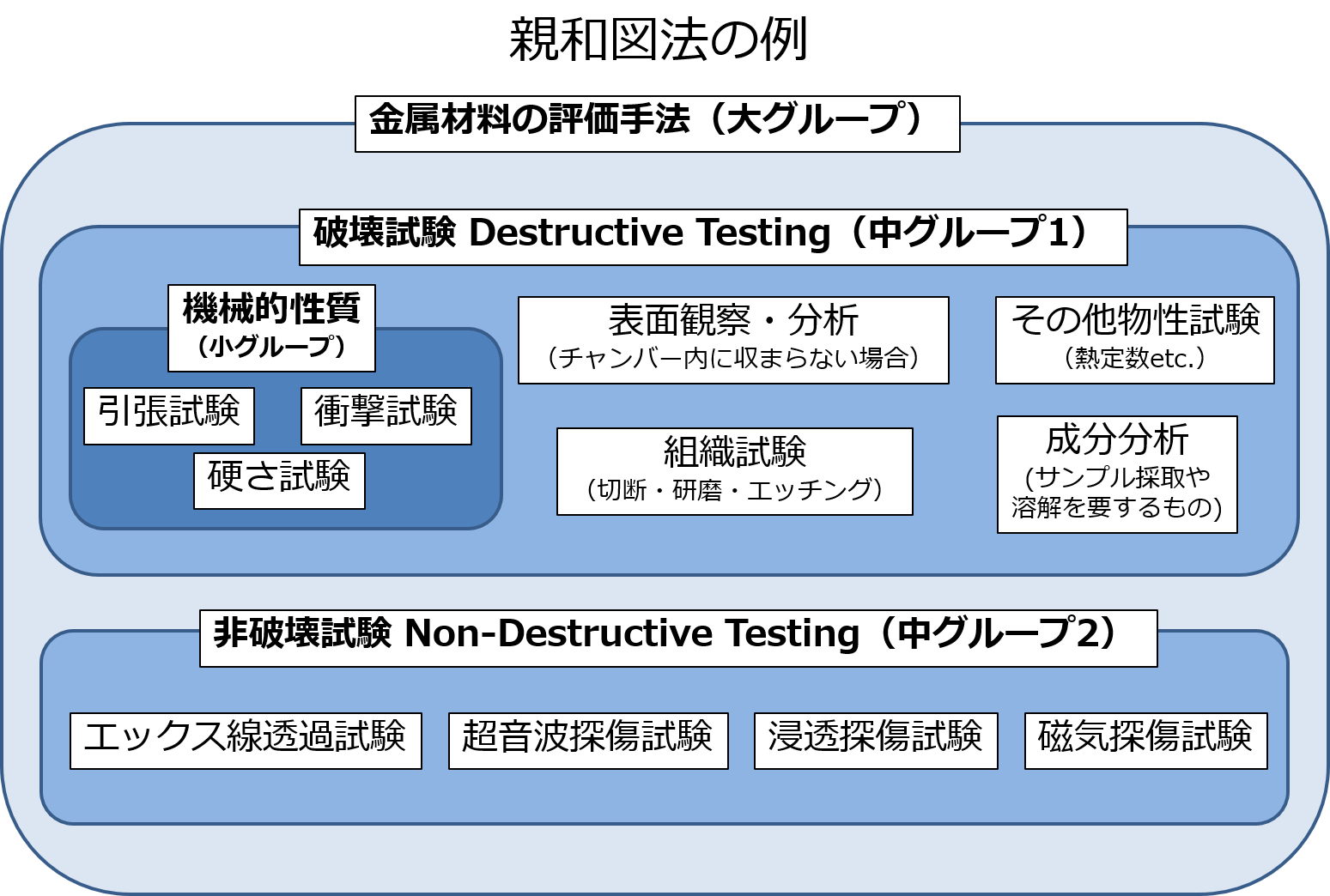
親和図法
親和図法は問題となる要因を親和性(関連性)の高いグループに分け、整理・体系化する手法です。
一つの要因では分からなかった課題を明確化し、問題の構造を掴むことができるといった特徴があります。
それでは、例を見てみましょう。
親和図法の例として、金属材料の試験方法を親和性でグループ分けしました。
「サンプルを壊して検査する破壊試験」と「サンプルを壊さずに検査できる非破壊試験」とで分けました。
破壊試験は、さらに「機械的性質」などの小グループを作って部分的に分類の粒度を細かく分類するのもいいでしょう。
製品製造において一定程度の品質を保証したり、研究用途で特性を評価する必要がありますよね。
その際、どうしても壊せない事情がある場合、非破壊試験を実施します。
非破壊試験は、内部欠陥や内部構造の把握が主な目的となります。
最近では、図面が手に入らない製品のリバースエンジニアリング目的でX線CTなどで非破壊試験を実施し3Dデータを取得するなどして3Dプリンターで再現するなんて用途もありますね。
また、引張強さ・伸び・硬さといった物性値が数値として必要な場合などは、必然的にサンプルを壊さざるを得ないため、破壊試験を実施する必要があります。
当然ながら、製造工程の全数検査などでこれをやってしまうと何一つ製品が作れませんので、抜き取りなど検査数を制限する必要がありますね。
もう少し一般的な場面を想定するならば、グループディスカッションで「ブレーンストーミング」なんかをする時にもかなり使えますよ。
一人一人の意見を付箋紙に書き、ホワイトボードに親和性の高いグループごとにまとめて貼り付けると、議論の方向性がクリアになります。
是非様々な場面で活用できる手法ですのでお試しあれ!
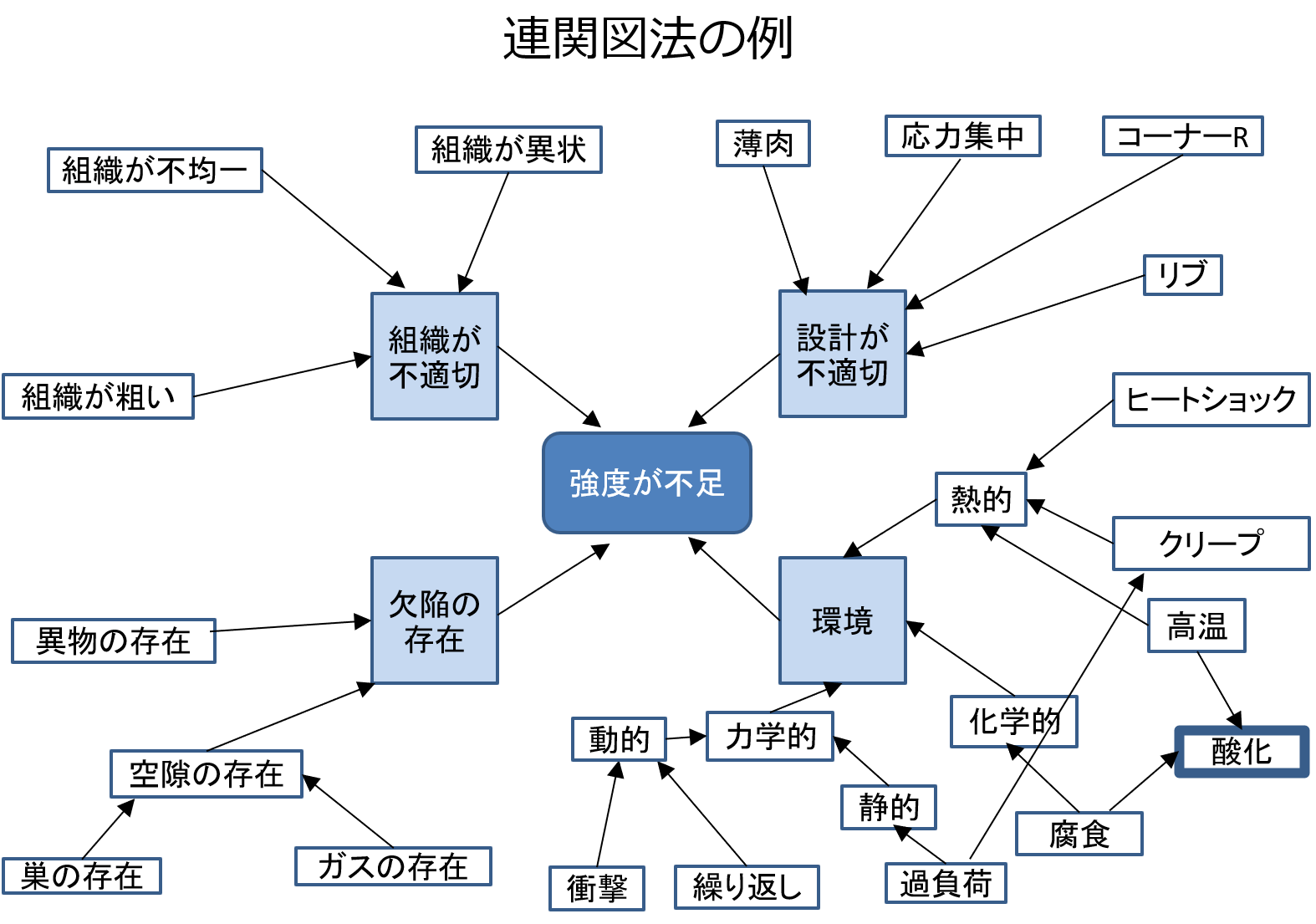
連関図法
原因ー結果、目的ー手段などが複雑に絡みあった問題の因果関係を論理的につなぐことで問題を明らかにする手法です。
要因と要因を矢印で結び、因果関係を見つけた上で主要因を追求することが主な目的です。
それでは例を見てみましょう。
金属材料の「強度不足」という現象(結果)を例に、その原因となる事象を周囲に書き出し、さらにその原因や関連事項を書き出し、有機的につないでいることが分かります。
深堀していくことで、周囲に関連事項が広がり、矢印で示される関連性が複雑になっていくイメージです。
どこまで粒度を細かくするかは、連関図法を用いる目的に応じて、という事になります。
目安として、問題点がはっきりとし、実行可能な解決策まで落とし込めるところまで広げられるといいですね。
重要要因と考えらる事項については太枠で囲むなどするといいですね。
ここで、連関図法の作成手順を下記のようにまとめます。
- 問題内容を用紙の中央に書き、楕円で囲みます。
- 問題を引き起こしている原因を探り、四角の枠で囲んで書きます(1次原因)。
そして原因から結果(問題)へ矢印線を引きます。 - 出来るだけ多くの一次原因を書き込みます。
- 一次原因を引き起こしている更なる原因を探り、四角の枠で囲んで書きます(二次原因)。
そして原因から結果へ矢印線を引きます。 こうして更に下位の原因を書き込んでゆきます。 - 因果関係を探っていき、相互に関連していれば矢印線を引きます。
- 最後に、影響が大きい要因を決定してゆきます。末端にある要因や関係線の出入りが多い要因は重要要因候補です。
- 重要要因は太枠で囲います。ここが問題解決ポイントになります。
以上のような手順です。
要は、できるだけ多く原因を書き出し、現象間の関係性を矢印で示し、重要要因に辿り着くまでこの作業を行うという事です。
「原因ー結果」という関係性で例を見てきましたが、「目的ー手段」といった関係性でも使えますので是非様々なシーンで活用してみましょう!
系統図法
目的達成のために最適な手段や方法をツリー状に並べる手法です。
目的を達成するための手段を目的として捉え直すということを繰り返します。
その作業によって、目的と手段を多段階に展開でき最終的に実行するための手段にたどり着くことができます。
「目的ー手段」と階層的に展開するという点では連関図法と似ていますが、ちょっと違います。
連関図法は手段同士が連関し有機的なつながりをもって放射状に、あるいは複雑に展開していきます。
一方、系統図法は文字通り系統だって、図的に言うと左から右へ一方向に展開していくため、目的と手段という関係性がシンプルに整理されます。
このような特徴を押さえたうえで、系統図法の例を見てみましょう。
金属材料の「強度向上」というを最終的な目的と位置付けて左側に配置しています。
その手段や要因を右側に配置します。
右側に配置した手段や要因を今度は目的と捉え直すことで、さらに実行可能な細分化したプロセスに落とし込んでいくイメージです。
他の活用シーンとしては、組織やチームの目標から逆算して、大目標、中目標、小目標とブレークダウンすることで個々の目標に落とし込んだり、実行可能なアクションプランに落とし込むといったシーンが考えられます。
また、時系列的に展開するのであれば、5か年計画ー年次目標ー四半期目標ー月目標ー週目標ー今日やるべきこと、などといった展開も可能です。
このように系統図法は言語情報を階層的に整理することで視覚的にも分かりやすく整理できます。
自分の頭の中身を整理したり、他者へ説明する際にかなり有効な図法です。
さらに、系統図法的発想を身に着けておくと、頭の中でエアー系統図法が描けるようになり、論理的思考能力も高まります。
「それはあくまで手段であり、目的を先に明確化するべきです」
といった主張や、あるいは逆に
「それでは粒度が荒く目的の域に留まっています。もっと分解して実行可能なプランに落とし込まなくては何をしていいのか分かりません」
といった主張ができるようになります。
ディスカッションや第三者に説明するようなシーンでの説得力も強化されますので是非覚えておきたい図法の1つです!
PDPC法
事前に考えられる様々な結果を予測し、目標達成までに不測の事態が起こっても代替できる案を明確にしておく方法です。
途中段階の場合分けによって、辿るルートが異なる結果や判断も異なるケースがあります。
ちなみに、PDPCはProcess Dicision Program Chartの略です。
Processは過程、Decisionは決定、Programは計画、Chartは図です。
辿る道筋(過程)を決定するための計画図という事ですね。
よく、YES・NOで答える質問に順次答えて「あなたに合った○○は△△です」のような結論を導く質問紙がありますよね。
あれも一種のPDPC法です。
それでは、PDPC法の例を見てみましょう。
基本的には上から下に作業は流れます。
シンプルな図ではありますが、
〇:状態
□:対策
◇:分岐
→:経路
ー:時間のない経路
といったように、一定のルールに沿って書くのがポイントです。
ある「状態」に陥った時に毎回取るべき対策に悩むようでは時間や労力の無駄が生じます。
YES・NOの質問に答えることでプロセスをパターン化できる時にはぜひ作っておくといい図ですね。
作業標準書を作成する際なんかにも応用してもいいでしょう。
アローダイアグラム
複数の独立した作業や工程が連続して実施される際に、作業の日程計画を図形と数字で表現するためのフローチャート図です。
あるプロジェクトの「作業工程の設計図」であり、「作業順序を明確化するフローチャート図」でもあります。
アローダイアグラムはPERT図(Program Evaluation and Review Technique 図)とも言われます。
アローダイアグラムは簡単に説明するのがちょっとやっかいです。
まずは、イメージを掴むためにも例を見てみましょう。
具体的な場面の想定はしていませんが、イメージとしては上図のようになります。
何となく、左から右側に順番に流れるんだな、枝分かれもするんだな、程度のことはパッと見で分かると思います。
でも、ちょっと分かりづらいですね。
もう少し詳しく解説します。
- 各作業の矢印は、必ず前後で結合点と繋がっている
- スタートとゴールの結合点を除いて、結合点は必ず作業の矢印と繋がっている
- 結合点に付与する番号もしくはアルファベットは、作業の方向なりに大きくなる
- 結合点は、そこから出て再びその結合点に戻る作業経路を持ってはならない
- ある結合点から伸びる作業は、その結合点へ向かう事前作業がすべて終わっていないと取り掛かれない
- 並行作業がある場合は結合点を増設し、点線矢印によってダミー作業を設ける
というルールに沿って書きます。
1.~4.は結合点と作業はセットで存在し、左から右への一方通行というシンプルなことを説明しています。
ちょっとややこしいのが、5.と6.です。
このあたりは、「工程全体においてどの作業が律速(遅れの原因)か」を捉えると分かりやすいですよ。
〇結合点:作業と作業の合間の点
→矢印:「作業」を意味する。
所要時間(日数など)とセットで表記される。
→破線矢印:「ダミー作業」を意味する。
実作業は伴わないため、作業時間はゼロ
アローダイアグラムを構成する記号はシンプルです。
結合点と矢印のみの記号を使います。
- 最早結合点時刻
- 最遅結合点時刻
- 余裕日数
- クリティカルパス
ある作業について計画上最も早く開始できる時点。
最早結合点時刻は、まずプロジェクトの開始日をスタート地点に設定し、それ以降の全結合点について以下の式で求められる
※(最早結合点時刻)=(ひとつ前の結合点における最早結合点時刻) + (作業の所要時間)
計画上最も遅い作業開始時点であり、この時点より作業開始が遅れてはならない最後のタイミング(デッドライン)。
最早結合点時刻は、プロジェクトの納期をゴール地点に設定し、それ以前の全結合点について以下の式で求められる。
※(最早結合点時刻)=(ひとつ先の結合点における最遅結合点時刻) – (作業の所要時間)
各結合点において作業開始までに与えられる時間的余裕のこと。
つまり、「ある作業の締め切りまでに何日残っているか」という指標
※(余裕日数)=(最遅結合点時刻) – (最早結合点時刻)
アローダイアグラム全体を見渡したとき、スタート地点からゴール地点まで最も長く所要時間がかかる作業経路
これらの言葉の意味と計算方法を図から読み取れるようになると、アローダイアグラムの利用可能性が広がりますね。
クリティカルパス上で、余裕日数が大きく生じていた場合にどの”工程が律速か”などの分析に使えそうですね。
アローダイアグラムの活用場面
先ほど述べた通りアローダイアグラムは、プロジェクトにおける「作業工程の設計図」であり、「作業順序を明確化するフローチャート図」でもあります。
製造業の供給プロセス(サプライチェーン)には納期を遵守しなければならない工程が多いため、進捗管理におけるアローダイアグラムの採用は非常に効果的ですね。
事前の作業設計にはじまり、プロジェクト開始後もアローダイアグラムから得られる情報をもとにした軌道修正を行うなど、効率よく最短で目標を達成できるようなマネジメントを行うのに有効といえます。
マトリックス図法
マトリックス図法はある事象(結果)に影響を与える複数の要素の組み合わせの効果を表形式で表現した図です。
要素の数や、どの要素間の組み合わせを採用するかなどで型の形式はさまざまです。
二次元的な最もベーシックなL型は多くの方が作成された経験があるのではないでしょうか。
例を見てみましょう。
材料の高強度化を目的とした材料開発における場面を想定したL型マトリックス図です。
要素として「添加剤」と「熱処理」、それぞれABの2水準ずつの組み合わせとなります。
それらが評価項目である「効果」「コスト」「リードタイム」に対する影響を〇、×、△の3段階で評価しています。
〇、×、△にそれぞれ点数を対応させることで、ランク(総合評価)付けができます。
細かい議論はさておき、ざっくりと視覚的にどの組み合わせが最もパフォーマンスが高いかなどを表現したいときなどに重宝する図法ですね。
また、マトリックス図法はL型のみではありません。
下図のようにバリエーションはいろいろです。
目的に応じて使い分けましょう。
マトリックスデータ解析法
マトリックスデータ解析法は、主成分分析と同義です。
主成分分析は統計学上のデータ解析手法のひとつです。
多くの量的な説明変数を、より少ない指標や合成変数(複数の変数が合体したもの)に要約する手法です。
この要約は「次元の縮約」という表現で呼ばれることもあります。
要約した合成変数のことを「主成分」と呼びます。
ちょっとこれだけ説明されても分かりづらいですね。
わかりやすく言えば、たくさんの次元(指標)のデータから、全体をわかりやすく見通しの良い1~3程度の次元に要約していくことです。
たとえば、身長と体重という2次元から、BMI(ボディマス指数)という肥満度を表す1次元の指標に要約するのが主成分分析、と言えばイメージしやすいですね。
人間、ある事柄を評価するのに、多くの評価指標の点数を一気に見せられて正確に処理できるほど認知能力に長けていません。
ですが、1~3程度の指標に限定されていれば、大体の評価結果を掴めます。
そうすると評価対象の事柄が複数あっても比較も容易になりますね。
マトリックスデータ解析法の概略の説明はこの辺にし、例を見てみましょう。
_散布図.png)
これはあくまで、解析の最終結果です。
前項のマトリックス図法をそのまま、主成分分析にかけた結果となります。
細かい解説の前に、この図から解釈できることは以下の通り。
①第1主成分(横軸)は総合力を表す
∵寄与率が66%、つまり全評価特性の66%を説明している
②第2主成分(縦軸)は主に”効果”の評価特性を表す
∵第2主成分の効果の固有ベクトルが0.86
つまり、効果と第2主成分の相関係数は0.86と相関が強い
うーん、正直なんのこっちゃですよね。
途中の計算過程をすっ飛ばしてますので、無理もありません。
それでは、細かい解説に移ります。
ですが、マトリックスデータ解析法は他の新QC7つ道具より難解です。
ちょっと覚悟して臨みましょう(笑)
Step1.変数の単位を揃えるためにデータを規準化する
※標準化変量は、([値]−[平均値])÷[標準偏差]で求める
※標準化変量の算出は =STANDARDIZE(値, 平均値, 標準偏差)の関数が便利
Step2.規準化したデータの相関係数行列を求める
※EXCELのデータ分析の分析ツール「相関」を使うと便利(アドイン追加が必要)
Step3.相関係行列の固有値と固有ベクトルを求める
※固有値は手計算やEXCELでの計算は難しい
※統計解析ソフト「R]やCASIOが提供する計算サイト「Ke!san」が便利
Step4.因子負荷量を求める
Step5.主成分得点を求め、散布図を描く
となります。
Step1,2,4,5はMicrosoft ECXELなどで計算可能です。
Step3だけはEXCELでは難しく、さらに高度な統計解析ソフトなどが必要となります。
それでは、各Step毎の作業手順を用語の意味も確認しながら詳しく解説します。
Step0:マトリックスのスコア化・平均値・標準偏差の算出
まずは、解析の元になるデータがない事には、解析が進みませんので、Step0からスタートします。
下図が元データになります。
マトリックス図法で使用した図そのものですが、以下の点を改変しています。
- 数値解析するため、〇×△ではなく、点数(0~2点のスコア)に換算
- 各評価特性毎に”平均値”と”標準偏差”を算出
- マトリックスデータ解析法は主成分分析と同義である
∴評価特性の縮減が目的(できれば2軸で表現したい)
Step1:規準化
規準化とは「標準化変量」を算出することです。
標準化変量とは、以下のように定義づけられます。
(標準化変量)=(値 – 平均値)/ 標準偏差
= STANDARDIZE(値, 平均値, 標準偏差)
規準化を行うと、このようにマトリックス図を再整理できます。
勘の良い方は式を見ただけで分かると思いますが、規準化を行うと元のデータ固有の平均値や標準偏差の大きさに影響されない値が得られることになります。
本例では、0~2点しかとり得ないスコアですので、あまり規準化の意味がない感じですが、例えば”硬さ”と”引張強さ”などまったく次元の異なる評価指標も規準化により一色単に扱えるようになります。
Step2:規準化したデータの相関係数行列の算出
相関係数行列とは、各変数同士の相関係数を行列形式の表にまとめたものです。
相関係数とは、変数同士の相関の強さを数値化したのもで、-1~+1の値を取り得ます。
-1に近いほど負の相関が強く、+1に近いほど正の相関が強いことを表します。
規準化したデータの相関行列を示します。
.png)
上図から以下のことが読み取れます。
- 同じ変数同士の相関は、当たり前ですが+1となります
- コストとリードタイムは-0.85で”負の相関”が強いことがわかる
尚、相関係数行列はEXCELの[分析]メニュー/ [データ分析]ツール/ [相関]が便利です。
※分析ツールを有効化するにはアドイン追加が必要
Step3:相関係数行列の固有値と固有ベクトルを求める
ここから、ちょっと用語の意味が難しくなるのと同時に計算もかなり厄介になります。
まず用語の説明から。
固有値:その主成分が元の特性データ全体の変動をどの程度代表しているかを表す値
固有ベクトル:各主成分において各評価特性がどの程度影響を及ぼすか重みの値
寄与率:全体の変動を100%として固有値を%表示したもの
となります。
用語の意味を押さえたうえで、計算結果を見てみましょう。
この計算結果から読み取れる情報は、
- 第一主成分でデータ全体の7割弱(66%)説明できる
- 第二主成分でデータ全体の3割(31%)説明できる
- つまり第一主成分と第二主成分合わせてデータ全体の9割程度説明できる
ということ。
これはいい傾向ですね。
第一主成分と第二主成分だけでデータの9割が説明できるという事は、この2つの成分を軸にとれば2軸で表現できます。
つまり、平面的なグラフだけで9割の説明が片付くわけです。
良い予感がします。
固有値、固有ベクトル、寄与率を求める際の注意点を以下に示します。
- 固有値の計算は手計算やEXCELでは厳しい
- 統計解析ソフト「R」やCASIOが提供する計算サイト「Ke!san」が便利
- 主成分をどこまで求めるかは累積寄与率が80%を超えるのが目安とするのが一般的
累積寄与率8割越えが目安なので、本例では第二主成分までで9割ですから、第二主成分までの計算で十分という解釈になります。
Step4:因子負荷量を求める
因子負荷量は下記の指揮で定義されますが、「相関係数」と同義です。
(因子負荷量)=(固有ベクトル)×(各主成分の固有値の平方根)
※元の変数と主成分との”相関係数“と同義
因子負荷量の計算結果を示します。
因子負荷量の計算はシンプルですので、EXCELなどでサクっとできてしまいます。
上図から
- 第1主成分とリードタイムとの間に強い相関(0.98)がある
- 第2主成分と効果との間に強い相関(0.86)がある
ということが読み取れますね。
説明変数を縮減して主成分にまるめてしまったわけですが、因子負荷量を見ることによって各主成分にどのような意味が含まれるかを読み解くことができるというわけです。
つまり、第一主成分の値が大きいという事は、主にリードタイムでのスコアが高いんだな、と解釈できることになります。
Step5:主成分得点表を求め、散布図を描く
いよいよ最終局面です。
主成分得点表を作成し、散布図上にプロットします。
ちなみに、Step5ではStep4の因子負荷量を計算で使うことはありませんが、主成分の意味を解釈する上で重要なのでStep4で計算しています。
主成分得点って何?
ということで下のように定義します。
主成分得点(各手法毎)= Σ(各評価特性の固有ベクトル)i×(規準化した第i特性値データ)
ちょっと面倒ですが、このように計算します。
この式に当てはめると下のようにまとめられます。
さらに散布図上にプロットするとこうなります。
ちょっと長かったですが、これがマトリックスデータ解析法(主成分分析)で得たかった図になります。
改めて、この図から読み取れることを確認します。
①第1主成分(横軸)は総合力を表す
∵寄与率が66%、つまり全評価特性の66%を説明している
②第2主成分(縦軸)は主に”効果”の評価特性を表す
∵第2主成分の効果の固有ベクトルが0.86
つまり、効果と第2主成分の相関係数は0.86と相関が強い
本例では、”効果”、”コスト”、”リードタイム”という3つの評価指標(説明変数)を第一主成分、第二主成分という2つの主成分に縮減(3→2)に縮減という例を示しました。
実用的にはもっとたくさんの説明変数を2つ3つの主成分に縮減して、複雑なデータをコンパクトに説明するのに役立てたりできます。
評価項目が複数あり、各要素の比較が難しい場面などに遭遇したらぜひ使ってほしい解析法です!
まとめ
いかがでしたでしょうか。
新QC7つ道具について実例を交えながら見てきました。
新QC7つ道具は最後に紹介したマトリックスデータ解析法以外は言語データなどの定性的な分析です。
思考の整理や話し合いのまとめなどにも応用できます。
ここでざっくりおさらいしましょう。
- 親和図法
- 連関図法
- 系統図法
- PDPC法(Process Decision Program chart)
- アローダイアグラム
- マトリックス図法
- マトリックス・データ解析法
問題となる要因を親和性(関連性)の高いグループに分け、整理・体系化する手法。
一つの要因では分からなかった課題を明確化し、問題の構造を掴むことができる。
原因ー結果、目的ー手段などが複雑に絡みあった問題の因果関係を論理的につなぐことで問題を明らかにする手法。
要因と要因を矢印で結び、因果関係を見つけた上で主要因を追求する。
目的達成のために最適な手段や方法をツリー状に並べる手法。
目的を達成するための手段を目的として捉え、その作業によって、目的と手段を多段階に展開でき最終的に実行するための手段にたどり着く。
事前に考えられる様々な結果を予測し、目標達成までに不測の事態が起こっても代替できる案を明確にしておく方法。
複数の独立した作業や工程が連続して実施される際に、作業の日程計画を図形と数字で表現するためのフローチャート図
問題としている事象の中から、対になっている要素を見つけ出して、これを行と列に配列し、その二元素の交点に各要素の関連の有無や度合いを表示することによって問題解決を効果的に進めていく方法。
説明変数の次元の縮減を目的とする主成分分析と同様の分析。
新QC7つ道具で唯一、定量データの解析を行う手法。
以上まとめでした。
“新”が付かない通常のQC7つ道具の説明は下記の記事を参照ください。

また、品質管理検定に関する記事としてこちらも参照してください。

参考書籍おすすめ書籍
QC7つ道具や新QC7つ道具を含めた品質管理手法・統計的手法・役立つフレームワークを学ぶには品質管理検定の受験がオススメです!
品質管理検定を受験するにあたってオススメしたい本を紹介します。
というより、私が実際に統計学や品質管理の知識がほぼゼロの状態からQC検定3級~1級合格まで使用した本の全てです。
予備知識なし、統計アレルギーの状態からこれらの本だけでQC検定1級までこぎつけましたので、まぁどのような方でもここで紹介する本を読んで解いてもらえれば十分かと思います。
全部並べるとこんな感じ。

カテゴリ別に紹介しますね。
テキスト&問題集として使用した本を並べるとこんな感じ。

そうなんです。
3級はテキスト使ってません。
取りあえず2級のテキストから入って、3級は問題集しかやってません。
実際それで十分でした。
時間とお金を節約したい方は真似してみて下さい。
テキストは以下2冊。
- 「一回で合格! QC検定2級 テキスト&問題集」 著者:高山均 発行所:成美堂出版
- 「品質管理検定集中講座[1]【新レベル表対応版】QC検定受験テキスト1級」 著者:稲葉太一ほか 発行所:(株)日科技連出版社
QC検定は半分が計算問題です。
手法偏(計算問題)はどうしても実際に手を動かして解いた量が本番で活きてきます。
そのようなこともあり、問題集は多めに解きました。
実践編(知識問題)だけであれば、そんなに問題を解く必要もないかなという感じもしますが。。。
問題集は以下4冊。
- 「一回で合格! QC検定3級 実戦問題集」 著者:高山均 発行所:成美堂出版
- 「過去問題で学ぶQC検定2級 ○○○○年版」 監修:仁科健 発行所:(一財)日本規格協会
- 「過去問題で学ぶQC検定1級 ○○○○年版」 監修:仁科健 発行所:(一財)日本規格協会
- 「品質管理検定講座 QC検定1級模擬問題集」 編著者:細谷克也 発行所:(株)日科技連出版社
副読本は絶対必須とまでは言いませんが、個人的には必要と感じています。
QC検定の受験対策に特化したテキストだけではどうしても問題を解く上で必要最低限の知識の解説に留まりがちです。
そこでオススメしたいのが以下2冊。

実践編(知識問題)だけであればテキストで十分ですが、手法偏(計算問題)についてはテキストではやや不十分です。
本質の理解が応用力や記憶力の定着に効いてきますし、そもそも手法偏で扱う統計学は実に奥が深いです。
知れば知るほど奥が深く自身の知識の無さに気づくほどです。
QC検定の勉強をしていく中で、
「ところで、この計算式、そもそもなんでこうなるの?」
と疑問にぶつかることがあります。
そんな時に役立つ副読本として、またより実践的に業務などで活かせるスキルとするために参考となる書籍を2つ紹介します。
- 「入門 統計学 ー検定から多変量解析・実験計画法までー」 著者:栗原伸一 発行所:(株)オーム社
- 「7日間集中講義! Excel統計学入門」 著者:米谷学 発行所:(株)オーム社




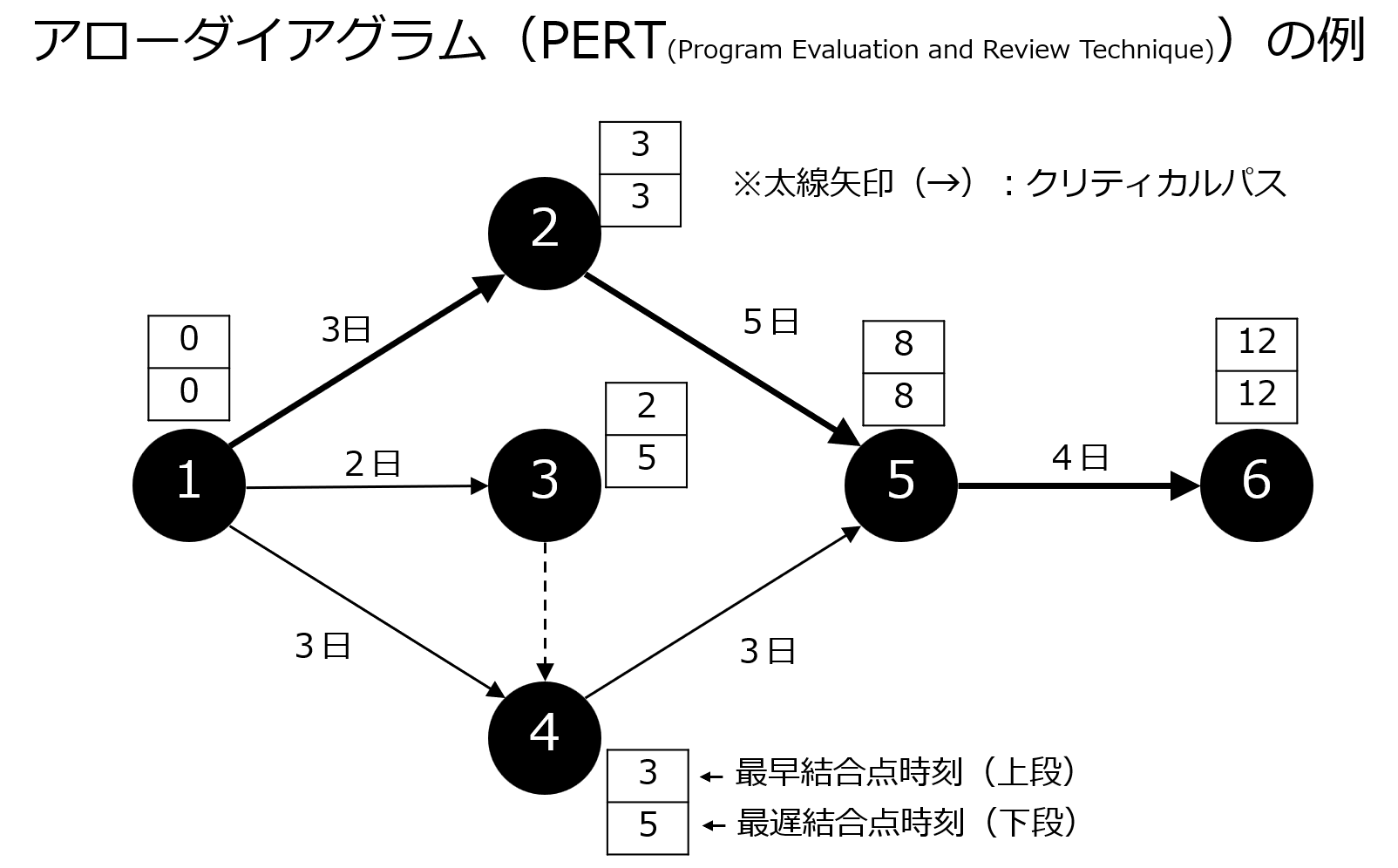


.png)
.png)
.png)
.png)
_主成分得点表.png)


コメント