はじめに ~使っていますか?QC7つ道具~
QC7つ道具使っていますか。
聞いたことくらいはあるでしょうか。
恐らく、製造にかかわるお仕事をされている方や品質保証部門などの方はいくつかの手法を既に使っていると思います。
実は、それらの方だけではもったいない!
QC7つ道具は様々な場面で応用可能です。
例えば、製造のみならず研究開発の場面はもちろん、市場調査や人口統計調査など経済学や社会学などでも使われていたりします。
別の記事

で紹介したQC検定でも、このQC7つ道具についての出題があります。
QC検定受験者のみならず、製造に関わる方以外でも多くの方に知っていただき、かつ使えそうなものから活用してもらいたいツールです。
ご存知の人はご存知でしょうが、QC7つ道具と”新”QC7つ道具があります。
新QC7つ道具については別の記事で紹介します。
ざっくりとした違いは
- QC7つ道具:主に定量的な解析(数値データ)に用いる
- 新QC7つ道具:主に定性的な解析(言語データ)に用いる
といった違いがあります。
が、あくまでざっくりとした分け方です。
QC7つ道具でも定性的な解析を行うツールもあれば、新QC7つ道具で定量的な解析を行うツールもあります。
どのツールが旧に、どのツールが新に属するかは覚える必要はありません。
思考ツール、解析ツールとして武器を増やしておくためにそれらの特徴と使い方をおさえておきましょう。
パレート図
パレート図はいわゆる「棒グラフ」と「折れ線グラフ」を組み合わせて1つのグラフ上に表したような見た目をしています。
“基本は棒グラフ”です。
では、普通の棒グラフと何が違うの?と疑問がわきますね。
その答えは、”折れ線グラフ”です。
って当たり前やないか!棒グラフと折れ線グラフの組み合わせってさっき言ったばっかりやん!
それはそうなのですが、パレート図のポイント以下2点を抑えることが重要です。
①グラフを左から降順に並べている
②折れ線グラフで累積比率を示している
です。
①で書いた通り、棒グラフは左から降順(左が大きく、右が小さい)でなくてはなりません。
つまり、棒グラフは右肩下がりとなります。
その理由が②に効いてきます。
全体を100%とした場合の累積比率が右に行くにつれて加算されていきます。
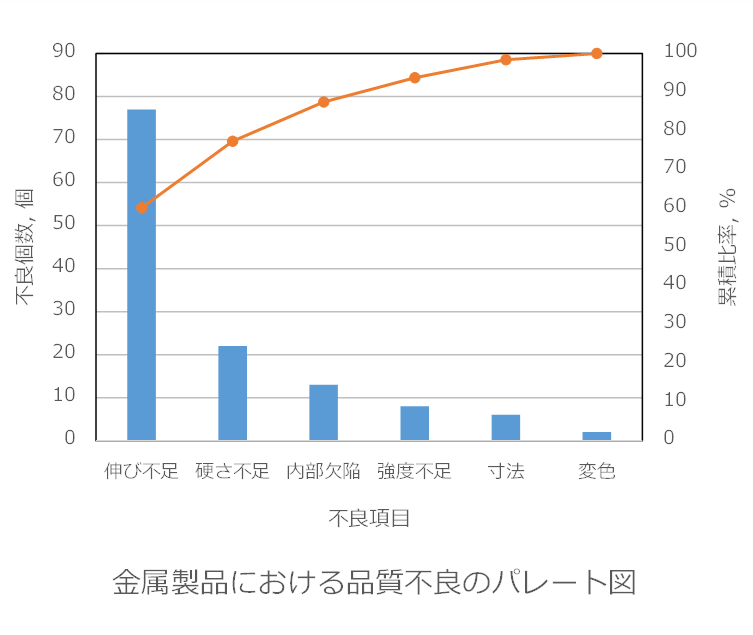
実際に例を見てみましょう。
で、何がパレート図において重要かという事ですが、
「問題の主要因が掴める」
という点です。
棒グラフだけでも視覚的に要因のきよどの大小がつかめますが、それをパレート図で補うことでより定量的に寄与率を把握することができます。
もっと言うと、
「この問題の要因の”8割”は○○と△△によるものだ」
と言ったように、累積寄与率をセットでグラフ上に表現することで考察が瞬時にできるのが特徴です。
パレート図の”パレート”って何でしょう?
以下の説明の通り、「パレート法則」からきています。
〇「パレートの法則」という考え方
物事を構成する要素の中で、一部の要素が全体の大部分に対して大きな影響を与えているという考え方です。
イタリアの経済学者ヴィルフレド・パレートによって1986年の論文で提唱されました。
影響を与える要素の割合が2割、その他の割合が8割と言われており「2:8の法則」とも呼ばれています。
この法則は、元々、経済学において「上位2割の富裕層が社会全体の富の8割を有し、残りの8割が2割の富を分け合っている」という富の偏在を意味しています。
現在ではこの考え方ではマーケティングや経済学など様々な分野、場面で用いられています。
なんとも面白く、かつ悲しくなるような法則ですね。
その法則をしっかり受け止めつつ、”本当の豊かさ”とは何かついつい考えてしまいます。
グラフ(管理図含む)
グラフはQC7つ道具の中でかなりざっくりした分類によるツールとなります。
ここでいうグラフは、いわゆる「点グラフ、折れ線グラフ、棒グラフ、円グラフなど、データ全体の傾向を示すもの」という総称的な意味で示しています。
先に説明したパレート図も、後に説明する散布図もいわばグラフなわけですが、その2つだけが特徴的である故、QC7つ道具では切り離されたと解釈しておくと良いでしょう。
点グラフ、折れ線グラフ、棒グラフ、円グラフなどは改めて説明する必要はないでしょう。
ただ1つ、かなり特徴的なグラフを含んでいるので、それは意識して覚えておきましょう。
それは、「管理図」です。
管理図は全く使ったことも見たこともない、という方もいるでしょう。
製造現場における製品の品質管理などの場面では良く使われるものです。
大枠としては折れ線グラフに含まれますが、その折れ線(プロット)の波形の特徴に対して統計的な観点からその安定度合いや危険信号などが読み取れるという優れたグラフです。
是非、どんなものか覚えておきましょう。
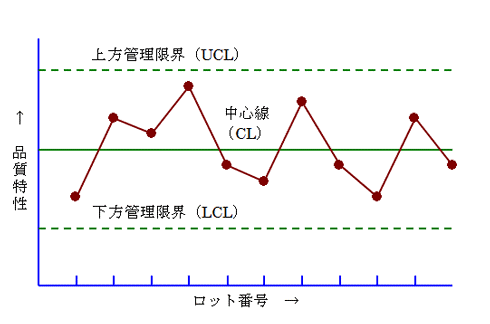
図 安定状態の管理図
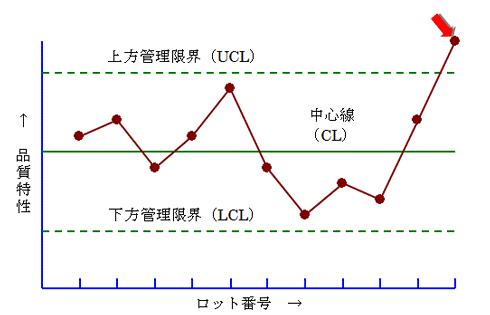
図 管理限界線の外に飛び出した管理図
管理図は工程が安定した状態にあるかを統計的にかつ視覚的にも捉えやすくまとめた折れ線グラフです。
横軸は時系列となり、ロッド番号などが対応します。
縦軸は品質特性となりますので、硬さ・強さなどの機械的性質、静電容量などの電気的特性、寸法など特性値であればなんでもOKです。
その他、管理図に欠かせないグラフの構成要素があります。
・中心線(CL:Center Line): 平均水準を示す
・上方管理限界線(UCL: Upper Control Limit):アクションの上方限界
・下方管理限界線(LCL: Lower Control Limit):アクションの下方限界
〇管理図の見方
打点されたプロットの”配置”と”分布”の2つの視点から、工程が”管理状態”にあるか”異常”かを判断する。
〇是正処置が必要な場合(異常と判断される場合)
・打点が管理限界外に飛び出したとき
・点の並び方が異常を示したとき
※単に管理限界線の外側に打点されたときだけではなく、点の並びが異常な時も是正措置を必要とする点に注意
〇妥当な管理限界線の幅
結論として、3σ法を採用します。
3σとは、標準偏差の3倍という意味です。
3σ管理図では、第1種の過誤を犯す確率は、通常0.3%程度です。
つまり、バラツキの分布が、正規分布(Normal distribution)であれば、99.7%はこの管理限界の中に入るという意味です。
〇管理図の種類
・管理図には取り扱うデータの質(計量値(連続値)か計数値(離散値)か)の違い
・X-R管理図、X管理図、Pn管理図、C管理図、U管理図など
があるが、ここでは割愛します。
詳しく知りたい人は、本記事の10章で紹介するの書籍などを参考にしてください。
チェックシート
チェックシートは特に説明の必要はありませんね。
下の図の通りです。
つまり、ある確認項目に対して、実施済みであれば□にチェックマークを入れ、未実施であれば空欄にしておく。
それだけです。
後で見返した時に未実施項目が一目でわかる、あるいは点検やタスクリストで何をしなければならないのか一目でわかる、そんな特徴があります。

ヒストグラム
度数分布図ともいいます。
区分(階級)ごとのデータまとまりを横軸に、発生頻度を縦軸に表します。
ヒストグラムは実に様々な場面で使われていますね。
私は写真が好きなのですが、デジタル画像の明るさやコントラスト調整を行う上でヒストグラムをよく使う、というか目にしますね。
デジタル画像は画素の集まりで、その画素1つ1つに輝度(明るさ)を持っています。
特定の輝度が何画素分あるか、それをグラフ化したのが画像処理で言うヒストグラムです。
その他の場面では人口統計などでも良く使いますね。
富士山型、釣り鐘型、つぼ型などのヒストグラムがあることは1度くらいは勉強したことがありますよね。
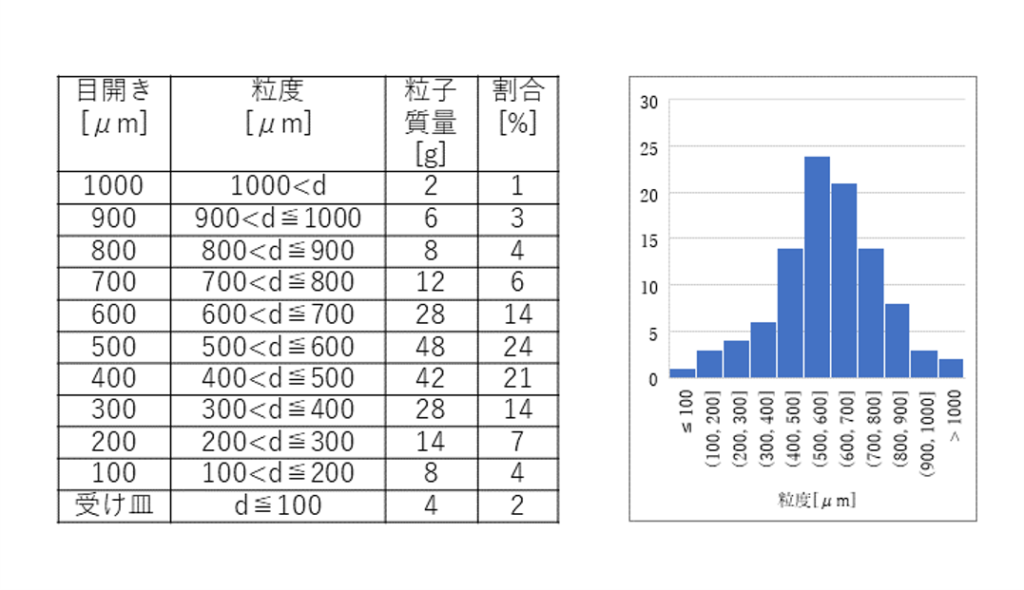
ここでは例として下記のようなヒストグラムを示します。
工業的には、砂などの粒状物の粒径を統計的にどのような分布を持っているかを確認する粒度分布試験といった試験がなされたりします。
最近ではレーザー回折などを使った試験もありますが、上の図は古典的な篩網を用いた方法の例となります。
グラフにおいて棒グラフの幅に相当するところを階級(上図では粒度)といいます。
その階級をどの程度のレンジに設定するかでグラフの形状や読み取れる情報が変わるため、適宜目的に沿った階級に設定する必要があります。
散布図
散布図!!
これはグラフの代表格と言ってもいいのではないでしょうか。
y = ax + b
といった関数(方程式)は中学校の数学で習う定番といった感じですよね。
このように2つの変数xとyの関係性を表すのになくてはならないのが散布図です。
関数をグラフ上に表現すると線を描くイメージですが、結局は線も集合として捉えられます。
1つ1つの点(プロット)が散布(分布)していることから散布図ですね。
点に近似曲線(近似直線)が引ければ、それは必然的に関数で表現できるというわけです。
それでは、例を見てみましょう
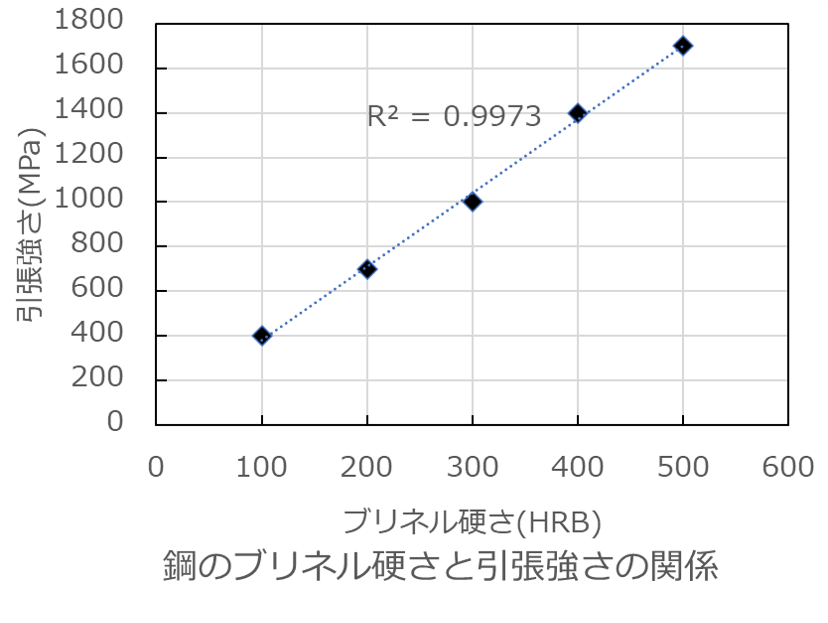
上の例だと鋼において硬さ(変数x)と引張強さ(変数y)との間に正の相関があることが分かりますね。
グラフ中に表示されている直線の横に”R2 = 0.9973″と書いてあります。
R2は決定係数とも呼ばれ、相関係数の2乗の値となります。
何のこっちゃ、という方は気にしないでください。
0 ≦R2≦1
の範囲を取りうる決定係数で、1に近いほど相関関係が強いという風に捉えておけば十分です。
上の例だとR2≒1ですのでかなり強い相関があります。
硬さを引張強さに変換できる範囲は限定的かもしれませんが、これだけ相関が強ければ引張試験を省略して硬さだけで管理することもできそうですね。
一般的なグラフの話に戻しますが、散布図の特徴としては2変数(横軸および縦軸として設定した変数)の「相関関係」が分かるところです。
例えば
xが増加すればyも増加する:正の相関
xが増加すればyは減少する:負の相関
といった具合です。
最小二乗法という方法を使えば、その比例関係を関数(回帰式)で表現することができます。
これを回帰分析と言ったりします。
これは手計算では難しいですが、EXCELなどを使うと非常に簡単にできますよ。
さらにEXCELを使うと2変数間の回帰式を求める単回帰分析のみならず、3変数以上の変数を取り扱う重回帰分析も結構簡単にできます。
こちらに関しては別の記事で紹介したいと思います。
特性要因図
結果と原因(要因)の関係を図式化したものです。
これかなり使えますよ!!
特性要因図はその形からフィッシュボーンダイアグラム(Fish Bone Diagram:魚の骨図)などと呼ばれたりもします。
例を見てみましょう。
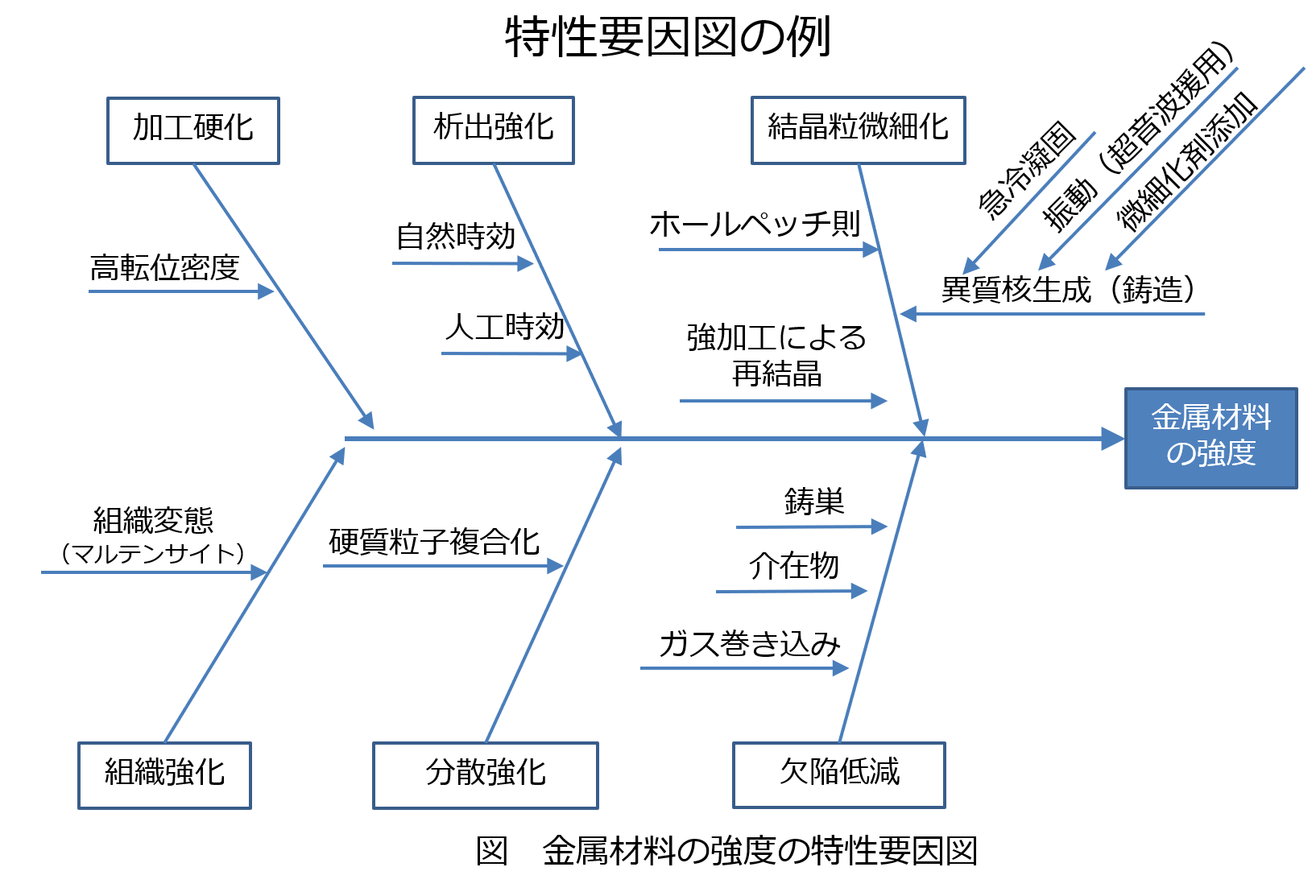
書き方に絶対的決まりはありませんが、基本的な書き方を示します。
①右側に現象の最終的な”結果”や”目的”を書く
②その結果や目的に向かって長い矢印(「矢印0号」とします)を書く
③結果や目的の”一次要因”や”一次手法”を周囲に書きだします
④それらの一次要因や一次手法から矢印0号に向かって矢印2号を引く
⑤今度は一次要因や一次手法に対する更なる”二次要因”や”二次手法を書き出す”
⑥二次要因や二次手法から一次要因や二次要因に向かって矢印3号を引く
⑦あとは必要に応じて、細分化できるところまで⑤と⑥を繰り返す
こんな感じです。
特性要因図は数値は取り扱わず、定性的なデータ整理法となります。
思考法、あるいは頭の中身を可視化して他者へ説明するなどといった目的に合った図法ですね。
もやっとした頭の中身がすっきりし、他者への説明も楽になります。
是非様々な場面で取り入れたいツールの1つです。
層別
結果(品質など)に影響する「原因」と「影響度」を把握するなどの目的で、小さいグループに分けて影響度やばらつきを比較する。
この小さいグループに分ける作業を「層別」といいます。
なので、層別に関しては
「層別という図法があります」
というよりは、
「層別してこのような表やグラフを書きました」
といったように”層別”という作業そのものを指しますので、一見イメージしずらいかもしれません。
似たような言葉で「分類」という言葉がありますね。
その分類と層別の違いを捉えることで理解が進みます。
※「層別」と「分類」の違い
分類とは、”あらかじめ用意された”カテゴリーに従って試料を仕分ける方法および行為なので、層別とは似ているが同じ意味ではない。
層別とは、データを年齢別などの同じ共通点を持つグループに分類すること。層別に分けることで、漠然としたデータの特徴がはっきりする。
このように分類との言葉の違いを意識した上で具体的な層別の例を見てみましょう。
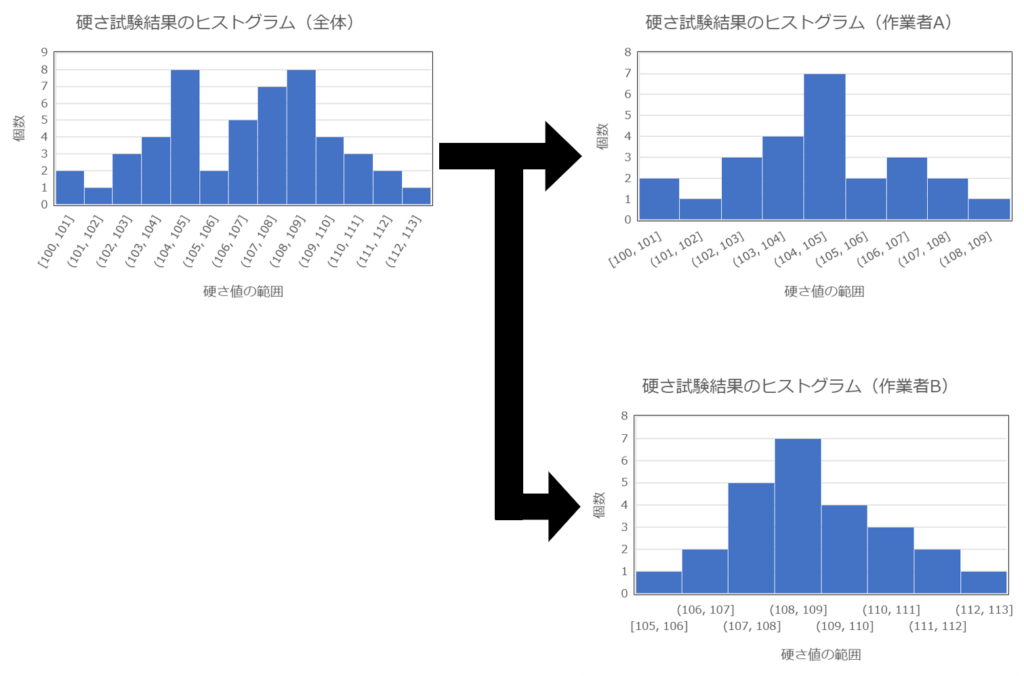
上の例は、同一の材質・処理を行った硬さサンプルの試験結果(n=50)を示しています。
同一の材質・処理を行った硬さ試験結果より、データばらつきが大きいことが問題となっていました。
ヒストグラム(全体)を見ると分布に特徴(山2つ)があることが分かります。
その不自然な特徴がなぜ出てくるのか、”層別”を行い検証することにしました。
作業者毎に層別してヒストグラムを作り直すと、右側のように分布を分離でき、作業者の違いによる傾向が表れた。
このように、「層別」を行うことで当初は様々なデータを混ぜて集計していたものを、何らかのグループで分けて(層別して)集計し直すことで、問題の要因や傾向を掴んだりするのに役立つ手法です。
まとめ ~けっこう便利でしょ?~
いかがでしょうか。
QC7つ道具は品質管理目的のみならず、様々な場面で活用ができるものが多く、既に使っているものなどもあったのではないでしょうか。
いくつかこのようなフレームワークを自身のツールとして持っておくことは、
・とっさにデータ整理をしなくてはならない
・複雑な現象を解析的に整理して分かりやすく咀嚼する
などといった場面で非常に有効です。
ここでざっとQC7つ道具の特徴を復習しましょう。
・パレート図
項目別に層別し、出現頻度(左縦軸)の大きい順に並べるとともに累積和(右縦軸)を示した図
・グラフ(管理図含む)
点グラフ、折れ線グラフ、棒グラフ、円グラフなど、データ全体の傾向を示すもの
・散布図
2変数間の関係を点グラフとして示したもの
・ヒストグラム
度数分布図ともいう。区分ごとのデータまとまりを横軸に、発生頻度を縦軸に示す。
・特性要因図
フィッシュボーンダイアグラムともいう。結果と原因(要因)の関係を図式化したもの
・チェックシート
チェック項目とチェックボックスを表で示したもの
・層別
結果(品質など)に影響する「原因」と「影響度」を把握するなどの目的で、小さいグループに分けて(層別)、影響度やばらつきを比較するもの
このような情報発信ブログやサイトなどで都度調べるのもいいですが、せっかくなのでQC検定(品質管理検定)を受験してみることをオススメします。
QC7つ道具をはじめとした統計的手法による解析スキルが身に付くばかりでなく、品質管理を行上での管理体制の構築の仕方など実践的な知識も系統だてて身に付きますよ!
詳しくは下記の記事を参考にしてください。

参考書籍おすすめ書籍
~テキストとして~
- 「一回で合格! QC検定2級 テキスト&問題集」 著者:高山均 発行所:成美堂出版
- 「品質管理検定集中講座[1]【新レベル表対応版】QC検定受験テキスト1級」 著者:稲葉太一ほか 発行所:(株)日科技連出版社
~問題集として~
- 「一回で合格! QC検定3級 実戦問題集」 著者:高山均 発行所:成美堂出版
- 「過去問題で学ぶQC検定2級 ○○○○年版」 監修:仁科健 発行所:(一財)日本規格協会
- 「過去問題で学ぶQC検定1級 ○○○○年版」 監修:仁科健 発行所:(一財)日本規格協会
- 「品質管理検定講座 QC検定1級模擬問題集」 編著者:細谷克也 発行所:(株)日科技連出版社
~副読本として~
- 「入門 統計学 ー検定から多変量解析・実験計画法までー」 著者:栗原伸一 発行所:(株)オーム社
- 「7日間集中講義! Excel統計学入門」 著者:米谷学 発行所:(株)オーム社





コメント